A lady is pulling a big inflatable rubber ducky in from the lake. A rope is attached to a hook near the bottom of the ducky and the lady is standing on the dock and pulling the rope in at a rate of 3 ft/s. The height at which the lady is pulling the rope is 7 ft. higher than where the rope is attached to the ducky. How fast is the ducky approaching the dock when they are 100 feet apart? 4) a) Label the picture with any variables needed to define the variables you choose to use. dy dy b) Use Leibnitz notation (e.g., , etc.) to identify the rate you are given and the rate you need to find. Rate Given: Rate need to find: Set up an equation that relates the variables used in part (a) and then solve. Show all work and be sure to state your conclusion. c)
A lady is pulling a big inflatable rubber ducky in from the lake. A rope is attached to a hook near the bottom of the ducky and the lady is standing on the dock and pulling the rope in at a rate of 3 ft/s. The height at which the lady is pulling the rope is 7 ft. higher than where the rope is attached to the ducky. How fast is the ducky approaching the dock when they are 100 feet apart? 4) a) Label the picture with any variables needed to define the variables you choose to use. dy dy b) Use Leibnitz notation (e.g., , etc.) to identify the rate you are given and the rate you need to find. Rate Given: Rate need to find: Set up an equation that relates the variables used in part (a) and then solve. Show all work and be sure to state your conclusion. c)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Please explain step by step

Transcribed Image Text:**Problem 4:**
A lady is pulling a big inflatable rubber ducky in from the lake. A rope is attached to a hook near the bottom of the ducky, and the lady is standing on the dock, pulling the rope in at a rate of \(3 \, \text{ft/s}\). The height at which the lady is pulling the rope is \(7 \, \text{ft}\) higher than where the rope is attached to the ducky. How fast is the ducky approaching the dock when they are \(100\, \text{ft}\) apart?
**a) Label the picture with any variables needed to define the variables you choose to use.**
**b) Use Leibnitz notation (e.g., \(\frac{dy}{dx}, \frac{dy}{dt}\), etc.) to identify the rate you are given and the rate you need to find.**
- **Rate Given:** \(\frac{dy}{dt} = 3 \, \text{ft/s}\)
- **Rate to find:** \(\frac{dx}{dt}\)
**c) Set up an equation that relates the variables used in part (a) and then solve. Show all work and be sure to state your conclusion.**
**Diagram Explanation:**
The diagram shows:
- A lady on a dock pulling a rope attached to a rubber ducky in the water.
- The angle of the rope as it slopes down to the ducky.
- The height difference of \(7 \, \text{ft}\) between where the lady holds the rope and the point where it attaches to the ducky.
In this context:
- Let \(x\) be the horizontal distance between the dock and the ducky.
- Let \(y\) be the length of the rope.
- The relationship between \(x\), \(y\), and the \(7 \, \text{ft}\) height difference forms a right triangle.
- Use the Pythagorean theorem: \(x^2 + 7^2 = y^2\).
Differentiate with respect to time \(t\) to find the rate at which \(x\) decreases as the lady pulls the ducky closer.
Expert Solution
Step 1

Step 2
Sketch and labelled the diagram:
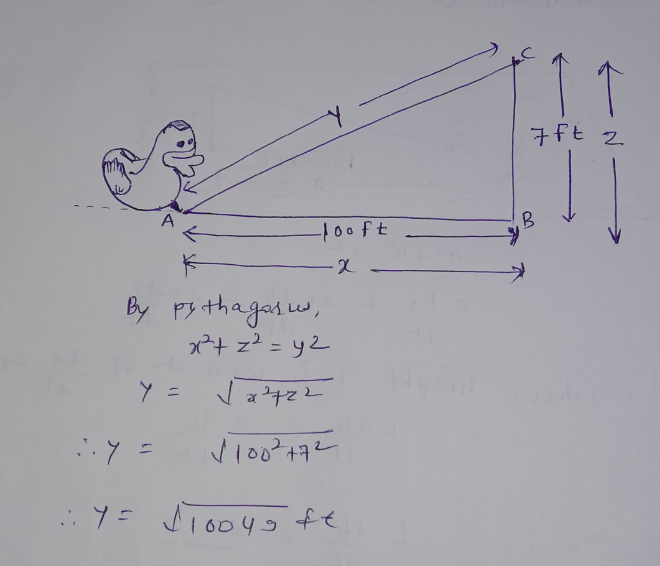
Step by step
Solved in 4 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

