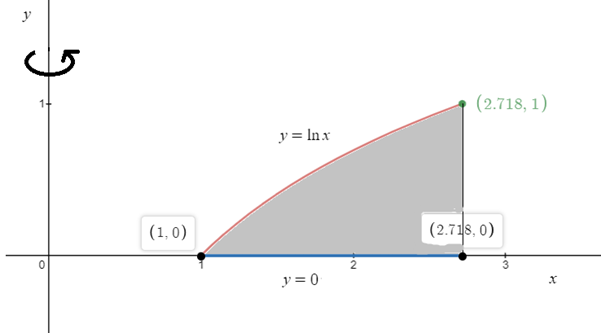
Find the area of the surface of revolution generated by revolving the graph of = In x ,bounded by y = 0 over the interval [1,e] about the y – axis. ET UP and SIMPLIFY THE INTEGRAL.DO NOT EVALUATE]
Unitary Method
The word “unitary” comes from the word “unit”, which means a single and complete entity. In this method, we find the value of a unit product from the given number of products, and then we solve for the other number of products.
Speed, Time, and Distance
Imagine you and 3 of your friends are planning to go to the playground at 6 in the evening. Your house is one mile away from the playground and one of your friends named Jim must start at 5 pm to reach the playground by walk. The other two friends are 3 miles away.
Profit and Loss
The amount earned or lost on the sale of one or more items is referred to as the profit or loss on that item.
Units and Measurements
Measurements and comparisons are the foundation of science and engineering. We, therefore, need rules that tell us how things are measured and compared. For these measurements and comparisons, we perform certain experiments, and we will need the experiments to set up the devices.
Please answer both questions and be detailed, thank you in advance!
![**Problem 6: Surface of Revolution**
**Objective:**
Find the area of the surface of revolution generated by revolving the graph of \( y = \ln x \), bounded by \( y = 0 \) over the interval \([1, e]\) about the \( y \)-axis.
**Instructions:**
Set up and simplify the integral. Do not evaluate the integral.
**Solution Outline:**
1. **Identify the function and bounds:**
- Function: \( y = \ln x \)
- Bounds: \( x \in [1, e] \)
- Revolving around the \( y \)-axis.
2. **Set Up the Integral:**
- The formula for the surface area \( S \) of a function \( x = g(y) \) revolved around the \( y \)-axis from \( y = c \) to \( y = d \) is:
\[
S = 2\pi \int_{c}^{d} x \sqrt{1 + \left( \frac{dx}{dy} \right)^2} \, dy
\]
3. **Rewriting the function:**
- Given \( y = \ln x \), we can express \( x \) as a function of \( y \): \( x = e^y \).
4. **Compute the derivative:**
- \(\frac{dx}{dy} = \frac{d}{dy}(e^y) = e^y\).
5. **Set up the integral with the appropriate bounds:**
- Since \( x = e^y \) when \( y \in [0, 1] \) (changing the bounds to match those for \( y \)):
\[
S = 2\pi \int_{0}^{1} e^y \sqrt{1 + (e^y)^2} \, dy
\]
6. **Simplify the integrand:**
- The integral becomes:
\[
S = 2\pi \int_{0}^{1} e^y \sqrt{1 + e^{2y}} \, dy
\]
By following these steps, we have set up and simplified the integral for the area of the surface of revolution. The integral is ready for evaluation.
**Note:** Since the instruction specifies not to evaluate the integral, we](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F7a908816-dcaf-4aa4-8dd6-7dd2f0aea84f%2Fdb864cc4-4325-4810-ae71-692e914d189a%2Fut41ak6.png&w=3840&q=75)
![### Problem 5: Arc Length of a Function
**Problem Statement:**
Find the arc length of the graph of \( y = \frac{1}{14} x^7 + \frac{1}{10x^5} \) over the interval \([1, 2]\).
**Solution Steps:**
To find the arc length of a graph \( y = f(x) \) over the interval \([a, b]\), we use the formula:
\[ L = \int_{a}^{b} \sqrt{1 + \left( \frac{dy}{dx} \right)^2} \, dx \]
1. **Function and Derivative:**
Given the function:
\[ y = \frac{1}{14} x^7 + \frac{1}{10x^5} \]
First, we need to calculate the derivative \( \frac{dy}{dx} \):
\[ \frac{dy}{dx} = \frac{d}{dx} \left( \frac{1}{14} x^7 + \frac{1}{10x^5} \right) \]
2. **Derivative Calculation:**
Using the power rule:
\[ \frac{dy}{dx} = \frac{1}{14} \cdot 7x^6 - \frac{1}{10} \cdot 5x^{-6} \]
\[ \frac{dy}{dx} = \frac{7}{14} x^6 - \frac{5}{10} x^{-6} \]
\[ \frac{dy}{dx} = \frac{1}{2} x^6 - \frac{1}{2} x^{-6} \]
\[ \frac{dy}{dx} = \frac{1}{2} x^6 - \frac{1}{2x^6} \]
3. **Arc Length Integral:**
Next, we plug the derivative into the arc length formula:
\[ L = \int_{1}^{2} \sqrt{1 + \left( \frac{1}{2} x^6 - \frac{1}{2x^6} \right)^2} \, dx \]
4. **Simplified Expression:**
We simplify inside the integral:
\[ \left( \frac{1}{](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F7a908816-dcaf-4aa4-8dd6-7dd2f0aea84f%2Fdb864cc4-4325-4810-ae71-692e914d189a%2Fcm5xw68.png&w=3840&q=75)
(6)
Plot the graph to find the region. The shaded area is the region.
Consider the formula to find surface area generated by revolution.
Find the derivative y’.
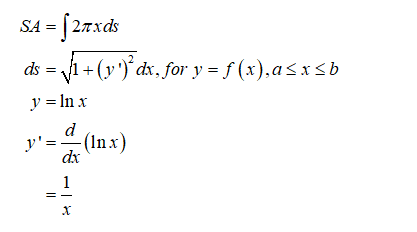
The interval for the integration is given.
Find the SA integral.
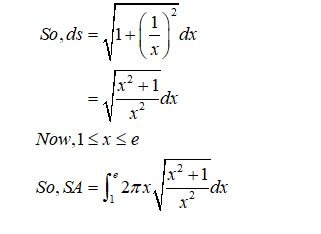
Simplify the integral using the properties for indefinite integration.
Use the trigonometric substitution method and simplify the integral.

Trending now
This is a popular solution!
Step by step
Solved in 7 steps with 7 images









