Homework Help is Here – Start Your Trial Now!
Math
Statistics
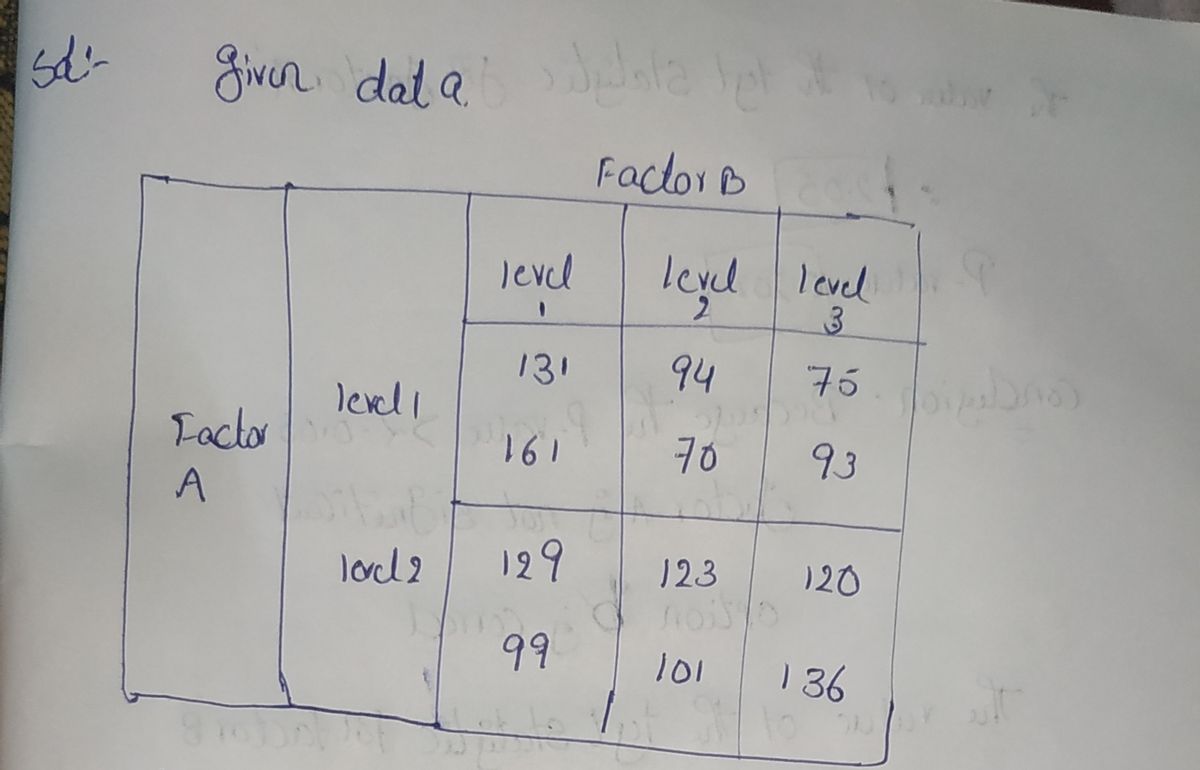
A factorial experiment involving two levels of factor A and three levels of factor B resulted in the following data. Factor A Level 1 Level 2 Level 1 131 161 129 99 Factor B Level 2 94 70 123 101 Level 3 75 93 120 136 Test for any significant main effects and any interaction. Use α = 0.05. Find the value of the test statistic for factor A. (Round your answer to two decimal places.) Find the p-value for factor A. (Round your answer to three decimal places.) p-value = State your conclusion about factor A. O Because the p-value > a = 0.05, factor A is significant. O Because the p-value > a = 0.05, factor A is not significant. O Because the p-value ≤ α = 0.05, factor A is not significant. O Because the p-value ≤ α = 0.05, factor A is significant. Find the value of the test statistic for factor B. (Round your answer to two decimal places.) Find the p-value for factor B. (Round your answer to three decimal places.) p-value =

A factorial experiment involving two levels of factor A and three levels of factor B resulted in the following data. Factor A Level 1 Level 2 Level 1 131 161 129 99 Factor B Level 2 94 70 123 101 Level 3 75 93 120 136 Test for any significant main effects and any interaction. Use α = 0.05. Find the value of the test statistic for factor A. (Round your answer to two decimal places.) Find the p-value for factor A. (Round your answer to three decimal places.) p-value = State your conclusion about factor A. O Because the p-value > a = 0.05, factor A is significant. O Because the p-value > a = 0.05, factor A is not significant. O Because the p-value ≤ α = 0.05, factor A is not significant. O Because the p-value ≤ α = 0.05, factor A is significant. Find the value of the test statistic for factor B. (Round your answer to two decimal places.) Find the p-value for factor B. (Round your answer to three decimal places.) p-value =

MATLAB: An Introduction with Applications
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
See similar textbooks
icon
Related questions
Question

The interaction questions please (The last 3)

 

A factorial experiment involving two levels of factor A and three levels of factor B resulted in the following data. Factor A Level 1 Level 2 Level 1 State your conclusion about factor A. = 131 161 129 99 Factor B Level 2 94 70 123 101 Level 3 75 93 120 Test for any significant main effects and any interaction. Use α = 0.05. Find the value of the test statistic for factor A. (Round your answer to two decimal places.) 136 Find the p-value for factor A. (Round your answer to three decimal places.) p-value = Because the p-value > a = 0.05, factor A is significant. Because the p-value > α = 0.05, factor A is not significant. Because the p-value ≤ α = 0.05, factor A is not significant. Because the p-value < α = 0.05, factor A is significant. Find the value of the test statistic for factor B. (Round your answer to two decimal places.) Find the p-value for factor B. (Round your answer to three decimal places.) p-value
Transcribed Image Text:A factorial experiment involving two levels of factor A and three levels of factor B resulted in the following data. Factor A Level 1 Level 2 Level 1 State your conclusion about factor A. = 131 161 129 99 Factor B Level 2 94 70 123 101 Level 3 75 93 120 Test for any significant main effects and any interaction. Use α = 0.05. Find the value of the test statistic for factor A. (Round your answer to two decimal places.) 136 Find the p-value for factor A. (Round your answer to three decimal places.) p-value = Because the p-value > a = 0.05, factor A is significant. Because the p-value > α = 0.05, factor A is not significant. Because the p-value ≤ α = 0.05, factor A is not significant. Because the p-value < α = 0.05, factor A is significant. Find the value of the test statistic for factor B. (Round your answer to two decimal places.) Find the p-value for factor B. (Round your answer to three decimal places.) p-value
Find the value of the test statistic for factor B. (Round your answer to two decimal places.) Find the p-value for factor B. (Round your answer to three decimal places.) p-value: = State your conclusion about factor B. Because the p-value ≤ α = 0.05, factor B is not significant. Because the p-value > α = : 0.05, factor B is not significant. Because the p-value > a = 0.05, factor B is significant. Because the p-value < α = 0.05, factor B is significant. Find the value of the test statistic for the interaction between factors A and B. (Round your answer to two decimal places.) Find the p-value for the interaction between factors A and B. (Round your answer to three decimal places.) p-value State your conclusion about the interaction between factors A and B. Because the p-value ≤ α = 0.05, the interaction between factors A and B is significant. Because the p-value > a = 0.05, the interaction between factors A and B is not significant. Because the p-value > α = 0.05, the interaction between factors A and B is significant. Because the p-value ≤ α = 0.05, the interaction between factors A and B is not significant.
Transcribed Image Text:Find the value of the test statistic for factor B. (Round your answer to two decimal places.) Find the p-value for factor B. (Round your answer to three decimal places.) p-value: = State your conclusion about factor B. Because the p-value ≤ α = 0.05, factor B is not significant. Because the p-value > α = : 0.05, factor B is not significant. Because the p-value > a = 0.05, factor B is significant. Because the p-value < α = 0.05, factor B is significant. Find the value of the test statistic for the interaction between factors A and B. (Round your answer to two decimal places.) Find the p-value for the interaction between factors A and B. (Round your answer to three decimal places.) p-value State your conclusion about the interaction between factors A and B. Because the p-value ≤ α = 0.05, the interaction between factors A and B is significant. Because the p-value > a = 0.05, the interaction between factors A and B is not significant. Because the p-value > α = 0.05, the interaction between factors A and B is significant. Because the p-value ≤ α = 0.05, the interaction between factors A and B is not significant.
Expert Solution
steps

Step by step

Solved in 5 steps with 5 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
MATLAB: An Introduction with Applications
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
Elementary Statistics: Picturing the World (7th E…
Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON
The Basic Practice of Statistics
The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman
Introduction to the Practice of Statistics
Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman
SEE MORE TEXTBOOKS