2. 4x-2y = -8 %3D 4x y = 2x + 4 %3D 241 -2
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:Certainly! Below is a transcription of the image suited for an educational website:
---
**Lesson: Solving Systems of Equations by Graphing**
**Example 2:**
*Equations:*
1. \( 4x - 2y = -8 \)
2. \( y = 2x + 4 \)
*Graph Description:*
The provided graph is a standard coordinate plane with x-axis and y-axis ranging from -6 to 6. Each axis is marked at intervals of 1 unit. This graph will be used to plot the given equations to find their point of intersection, which represents the solution to the system of equations.
*Solution Steps:*
1. **Rearrange Equation 1 into Slope-Intercept Form (y = mx + b):**
- Start with \( 4x - 2y = -8 \)
- Subtract \( 4x \) from both sides: \(-2y = -4x - 8\)
- Divide by -2: \( y = 2x + 4 \)
*Note:* In this case, both equations can be rewritten as \( y = 2x + 4 \), indicating that they might be the same line, and thus, there may be infinitely many solutions as they overlap completely.
2. **Graph the Equations:**
- Plot the equation \( y = 2x + 4 \) on the graph.
- Since both equations are identical, ensure the line represents both \( 4x - 2y = -8 \) and \( y = 2x + 4 \).
*Observation:*
If the lines overlap completely, the system of equations has infinitely many solutions, represented by all the points on the line \( y = 2x + 4 \).
*Conclusion:*
By graphing, you can visually identify the type of solution to the system of equations. Here, because the two equations are the same, it is clear that they represent the same line, hence infinitely many solutions exist.
---
Expert Solution
Step 1
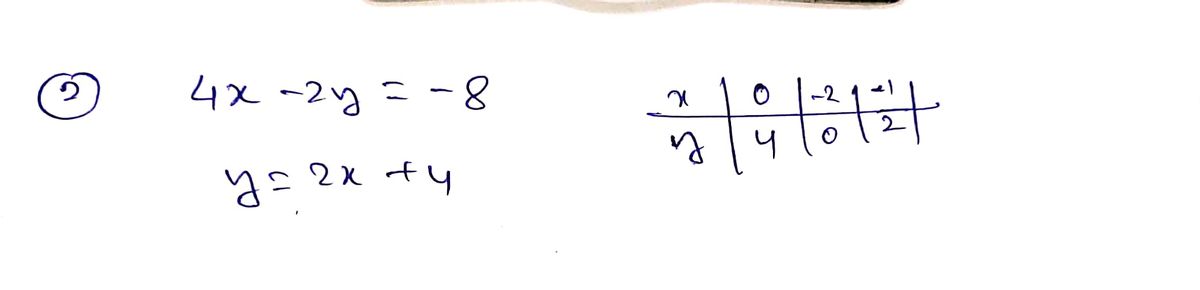
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

