A dietician read in a survey that 70.5% of adults in the U.S. do not eat breakfast at least 3 days a week. She believes that the proportion that skip breakfast 3 days a week is different than 0.705. To verify her claim, she selects a random sample of 71 adults and asks them how many days a week they skip breakfast. 44 of them report that they skip breakfast at least 3 days a week. Test her claim at a = 0.10.
Contingency Table
A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear relationship between two variables. A contingency table is indeed a type of frequency distribution table that displays two variables at the same time.
Binomial Distribution
Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.
![A dietician read in a survey that 70.5% of adults in the U.S. do not eat breakfast at least 3 days a week. She believes that the proportion that skip breakfast 3 days a week is different from 0.705. To verify her claim, she selects a random sample of 71 adults and asks them how many days a week they skip breakfast. 44 of them report that they skip breakfast at least 3 days a week. Test her claim at α = 0.10.
The correct hypotheses would be:
- \( H_0: p = 0.705 \)
- \( H_A: p \neq 0.705 \) (claim)
Since the level of significance is 0.10, the critical value is 1.645 and -1.645.
The test statistic is: [textbox] (round to 3 places)
The p-value is: [textbox] (round to 3 places)
The decision can be made to:
- ○ reject \( H_0 \)
- ○ do not reject \( H_0 \)
The final conclusion is that:
- ○ There is enough evidence to reject the claim that the proportion that skip breakfast 3 days a week is different than 0.705.
- ○ There is not enough evidence to reject the claim that the proportion that skip breakfast 3 days a week is different than 0.705.
- ○ There is enough evidence to support the claim that the proportion that skip breakfast 3 days a week is different than 0.705.
- ○ There is not enough evidence to support the claim that the proportion that skip breakfast 3 days a week is different than 0.705.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F635fc7d1-4125-4a99-970f-fc3f5300d520%2Fc8bb27c9-f57f-4415-bd52-0be94ada2f1e%2F7wfycqf_processed.png&w=3840&q=75)
It is need to be tested whether the population proportion of adults in U.S who do not eat breakfast at least 3 times in a week is different from 0.705 or not. This implies that test is two tail.
Thus, third option correct and hypothesis is,
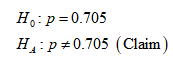
Step by step
Solved in 3 steps with 4 images









