A developmental psychologist is examining the development of language skills from age 2 to age 4. Three different groups of children are obtained, one for each age, with n = 18 children in each group. This data can be analyzed using a One Way ANOVA. Each child is given a language-skills assessment test. Answer the following questions
A developmental psychologist is examining the development of language skills from age 2 to age 4. Three different groups of children are obtained, one for each age, with n = 18 children in each group. This data can be analyzed using a One Way ANOVA. Each child is given a language-skills assessment test. Answer the following questions:
1) Identify the independent and dependent variable for the study.
2) Discuss why you should not use a Two Sample T-Test to answer this complex research problem.
The Hypothesis:
H0: There is no difference between the means of the three treatments.
Ha: There is a difference between the means of at least 2 of the treatments.
ANOVA Calculations
Total number of groups k = 3
Total children = 18 * 3 = 54
df between = k -1 = 3 - 1 = 2
df within = N - k = 54 - 3 = 51
SS between = 48 (given)
MS between = SS between / df betwween = 48/2 = 24
SS within = SS total - SS between = 252 - 48 = 204
MS within = SS within / df within = 204 / 51 = 4
F test = MS between / MS within = 24/4 = 6
The ANOVA Table is as below:
| Source | Sums of Squares | DF | Mean Squares | F |
| Between | 48 | 2 | 24 | 6 |
| Within | 204 | 51 | 4 | |
| Total | 252 | 53 |
The F critical: at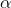 
= 0.01, df between = 2, df within = 51; Fcritical = 5.047
The Decision: Since F test is > F critical, we Reject H0.
The Conclusion: There is sufficient evidence at the 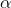= 0.01 to conclude that there is a significant difference between at least 2 of the treatments.
Step by step
Solved in 3 steps with 2 images
