A cylinder is rotating about an axis that passes through the center of each circular end piece. The cylinder has a radius of 0.110 m, an angular speed of 50.0 rad/s, and a moment of inertia of 1.26 kg·m2. A brake shoe presses against the surface of the cylinder and applies a tangential frictional force to it. The frictional force reduces the angular speed of the cylinder by a factor of 3 during a time of 8.00 s. Find the magnitude of the force of friction applied by the brake shoe.
A cylinder is rotating about an axis that passes through the center of each circular end piece. The cylinder has a radius of 0.110 m, an angular speed of 50.0 rad/s, and a moment of inertia of 1.26 kg·m2. A brake shoe presses against the surface of the cylinder and applies a tangential frictional force to it. The frictional force reduces the angular speed of the cylinder by a factor of 3 during a time of 8.00 s. Find the magnitude of the
Let ω0 denotes the initial angular speed, ω denotes the final angular speed, t denotes the time, and α denotes the angular acceleration. Therefore, the angular acceleration can be determined as,
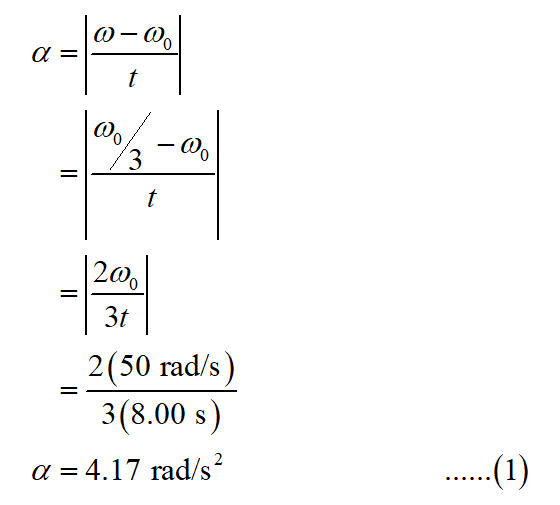
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images
