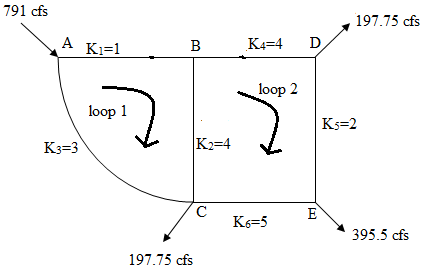
791 cfs 197.75 cfs K = 1 K=4 K = 5 197.75 cfs 395.5 cfs K = 3 K = 2
If the flow into and out of a two-loop pipe system are as shown in Figure. Determine the flow in each pipe using Hardy-Cross method. Value of n is 2.

Given :-
Coefficient of friction(K) in each pipes
K1=1
K2=4
K3=3
K4=4
K5=2
K6=5
n= 2 i.e. the number of iteration =2
According to Hardy cross method,
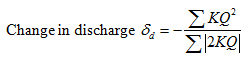
Where,
K= Coefficient of friction in pipe
Q= Rate of flow in pipe
KQ2= Frictional Force
Let us assume the initial flow rates in the pipe as following:-
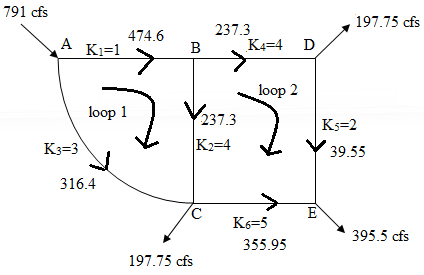
a) First Iteration
Let us consider Loop 1 i.e. ABCA first
(In clockwise direction flow will be positive and in anticlockwise direction flow will be negative)

Now, consider Loop 2 i.e. BDECB
(In clockwise direction flow will be positive and in anticlockwise direction flow will be negative)
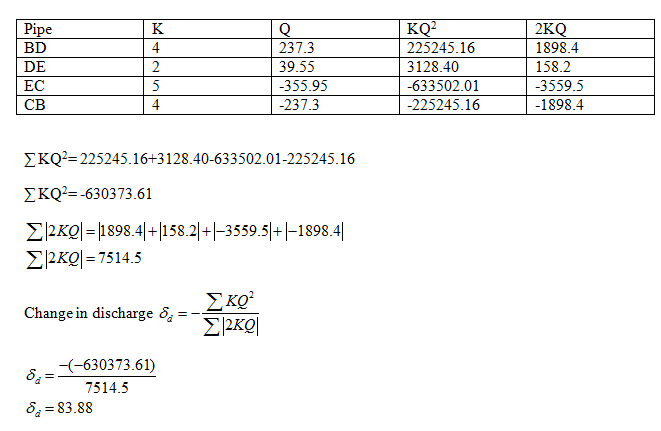
Step by step
Solved in 5 steps with 9 images









