Homework Help is Here – Start Your Trial Now!
Math
Algebra
5. Write a formula for the perimeter of the figure from problem #4 in terms of a, b, c, and d.

5. Write a formula for the perimeter of the figure from problem #4 in terms of a, b, c, and d.

Holt Mcdougal Larson Pre-algebra: Student Edition 2012
Holt Mcdougal Larson Pre-algebra: Student Edition 2012
1st Edition
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Chapter10: Measurement, Area, And Volume
Section10.2: Polygons And Quadrilaterals
Problem 1E
See similar textbooks
icon
Related questions
Question
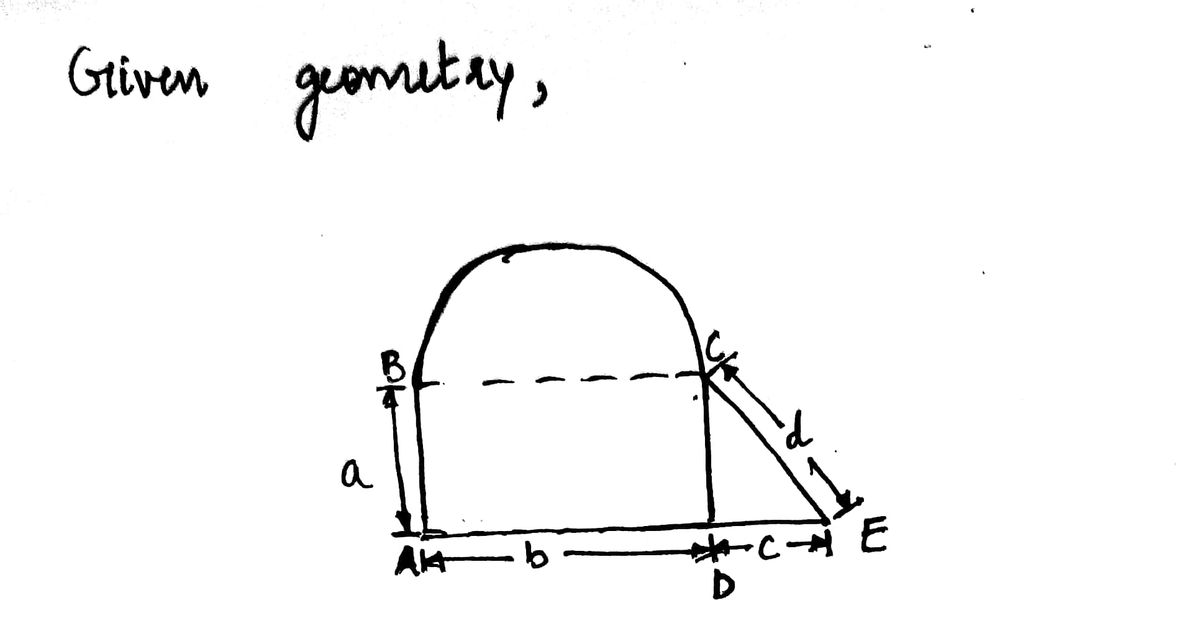
**Task 5: Perimeter Formula Calculation** **Objective:** Write a formula for the perimeter of the figure from problem #4 in terms of \( a, b, c, \) and \( d \). **Diagram Description:** The figure is composed of a rectangle with a semicircle on top. The rectangle has the following measurements: - Height: \( a \) - Base: \( b \) The semicircle sits on top of the rectangle, sharing its width. - The radius of the semicircle (half of the base of the rectangle): \( \frac{b}{2} \) A diagonal line extends from the top corner of the rectangle to the edge of the semicircle, labeled \( d \). **To find the perimeter:** 1. **Rectangle:** - One side of length \( a \) - One base of length \( b \) 2. **Semicircle:** - Perimeter: \( \pi \times \frac{b}{2} \) (half of the circle's circumference) 3. **Diagonal Line:** Length \( d \) Thus, the perimeter \( P \) can be formulated as: \[ P = b + 2a + \pi \times \frac{b}{2} - b + d \] \[ P = 2a + \left(\frac{\pi b}{2}\right) + d \]
Transcribed Image Text:**Task 5: Perimeter Formula Calculation** **Objective:** Write a formula for the perimeter of the figure from problem #4 in terms of \( a, b, c, \) and \( d \). **Diagram Description:** The figure is composed of a rectangle with a semicircle on top. The rectangle has the following measurements: - Height: \( a \) - Base: \( b \) The semicircle sits on top of the rectangle, sharing its width. - The radius of the semicircle (half of the base of the rectangle): \( \frac{b}{2} \) A diagonal line extends from the top corner of the rectangle to the edge of the semicircle, labeled \( d \). **To find the perimeter:** 1. **Rectangle:** - One side of length \( a \) - One base of length \( b \) 2. **Semicircle:** - Perimeter: \( \pi \times \frac{b}{2} \) (half of the circle's circumference) 3. **Diagonal Line:** Length \( d \) Thus, the perimeter \( P \) can be formulated as: \[ P = b + 2a + \pi \times \frac{b}{2} - b + d \] \[ P = 2a + \left(\frac{\pi b}{2}\right) + d \]
Expert Solution
Step 1

Algebra homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Holt Mcdougal Larson Pre-algebra: Student Edition…
Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL
Elementary Algebra
Elementary Algebra
Algebra
ISBN:
9780998625713
Author:
Lynn Marecek, MaryAnne Anthony-Smith
Publisher:
OpenStax - Rice University
College Algebra
College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897…
Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill
Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
Intermediate Algebra
Intermediate Algebra
Algebra
ISBN:
9780998625720
Author:
Lynn Marecek
Publisher:
OpenStax College
SEE MORE TEXTBOOKS