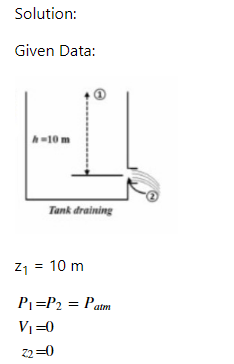
4. A tank is full of water and open at the top as shown in the figure. There is a frictionless nozzle near the bottom, the diameter of which is small compared with the diameter of the tank. Assuming the flow is steady, (1) What is the velocity of the flow out of the nozzle? 7/₂ dis de g=281~/3 V₂ = 12gh (1- lair (@Fluid) [ 1-(A₂/A₁) ² h-10 m (2) If the tank is full of CO2, what is the velocity of the flow out of the nozzle? Tank draining
4. A tank is full of water and open at the top as shown in the figure. There is a frictionless nozzle near the bottom, the diameter of which is small compared with the diameter of the tank. Assuming the flow is steady, (1) What is the velocity of the flow out of the nozzle? 7/₂ dis de g=281~/3 V₂ = 12gh (1- lair (@Fluid) [ 1-(A₂/A₁) ² h-10 m (2) If the tank is full of CO2, what is the velocity of the flow out of the nozzle? Tank draining
Elements Of Electromagnetics
7th Edition
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Sadiku, Matthew N. O.
ChapterMA: Math Assessment
Section: Chapter Questions
Problem 1.1MA
Related questions
Question
100%
plz help
![The equation displayed is:
\[ V_2 = \left[ \frac{2RT_1}{P_1M} (P_1 - P_{\text{atm}}) \right]^{1/2} \]
This mathematical expression calculates the velocity \( V_2 \) of a gas under specific conditions. Here's a breakdown of the variables used in the equation:
- \( R \) is the ideal gas constant.
- \( T_1 \) represents the initial temperature of the gas.
- \( P_1 \) denotes the initial pressure of the gas.
- \( M \) stands for the molar mass of the gas.
- \( P_{\text{atm}} \) is the atmospheric pressure.
The equation is structured to determine how these variables influence the velocity \( V_2 \) of the gas after a certain change from its initial state. The square root indicates that the final velocity is proportional to the square root of these factors.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff4dfc165-1571-419f-99fc-a4587d76c340%2F40600911-cf5c-48a5-b509-219a60bec227%2F4ro8loe_processed.png&w=3840&q=75)
Transcribed Image Text:The equation displayed is:
\[ V_2 = \left[ \frac{2RT_1}{P_1M} (P_1 - P_{\text{atm}}) \right]^{1/2} \]
This mathematical expression calculates the velocity \( V_2 \) of a gas under specific conditions. Here's a breakdown of the variables used in the equation:
- \( R \) is the ideal gas constant.
- \( T_1 \) represents the initial temperature of the gas.
- \( P_1 \) denotes the initial pressure of the gas.
- \( M \) stands for the molar mass of the gas.
- \( P_{\text{atm}} \) is the atmospheric pressure.
The equation is structured to determine how these variables influence the velocity \( V_2 \) of the gas after a certain change from its initial state. The square root indicates that the final velocity is proportional to the square root of these factors.
![### Educational Content on Fluid Dynamics
#### Problem Statement:
1. **Situation**: A tank is filled with water and open at the top. It includes a frictionless nozzle near the bottom, with the nozzle's diameter being small compared to the diameter of the tank. The flow is steady.
2. **Objective**:
- **(1)** Determine the velocity of the flow out of the nozzle.
- **(2)** Calculate the velocity if the tank is filled with CO₂.
#### Diagram Explanation:
The diagram shows a vertical tank labeled as "Tank draining." The water height is indicated as \( h = 10 \, \text{m} \). The tank is open at the top with a nozzle at the bottom. The notation \( d_1 > d_2 \) implies the tank's diameter is greater than that of the nozzle. The gravitational acceleration \( g \) is given as \( 9.81 \, \text{m/s}^2 \).
#### Velocity Calculation Formula:
For part (1), the velocity (\( V_2 \)) of the fluid (water) flowing out through the nozzle is calculated using the formula:
\[
V_2 = \left[ 2gh \left(1 - \text{Pair} \, ( \rho_{\text{Fluid}} ) \right) \right]^{1/2} \bigg/ \left[ 1 - \left( \frac{A_2}{A_t} \right)^2 \right]
\]
- **\( 2gh \)**: Represents the potential energy converted to kinetic energy.
- **\( \text{Pair} \, ( \rho_{\text{Fluid}} ) \)**: Accounts for pressure-related forces on the fluid.
- **\( \frac{A_2}{A_t} \)**: The area ratio of the nozzle cross-section (\( A_2 \)) to the tank cross-section (\( A_t \)), indicating that the nozzle's diameter is much smaller.
#### Considerations for CO₂:
For part (2), it is required to use the same fundamental principles but with the properties relevant to CO₂.
### Conclusion:
The task emphasizes understanding fluid flow through a nozzle using basic principles of fluid dynamics, such as Bernoulli’s equation, considering different fluids and flow conditions.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff4dfc165-1571-419f-99fc-a4587d76c340%2F40600911-cf5c-48a5-b509-219a60bec227%2Fws7gky_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Educational Content on Fluid Dynamics
#### Problem Statement:
1. **Situation**: A tank is filled with water and open at the top. It includes a frictionless nozzle near the bottom, with the nozzle's diameter being small compared to the diameter of the tank. The flow is steady.
2. **Objective**:
- **(1)** Determine the velocity of the flow out of the nozzle.
- **(2)** Calculate the velocity if the tank is filled with CO₂.
#### Diagram Explanation:
The diagram shows a vertical tank labeled as "Tank draining." The water height is indicated as \( h = 10 \, \text{m} \). The tank is open at the top with a nozzle at the bottom. The notation \( d_1 > d_2 \) implies the tank's diameter is greater than that of the nozzle. The gravitational acceleration \( g \) is given as \( 9.81 \, \text{m/s}^2 \).
#### Velocity Calculation Formula:
For part (1), the velocity (\( V_2 \)) of the fluid (water) flowing out through the nozzle is calculated using the formula:
\[
V_2 = \left[ 2gh \left(1 - \text{Pair} \, ( \rho_{\text{Fluid}} ) \right) \right]^{1/2} \bigg/ \left[ 1 - \left( \frac{A_2}{A_t} \right)^2 \right]
\]
- **\( 2gh \)**: Represents the potential energy converted to kinetic energy.
- **\( \text{Pair} \, ( \rho_{\text{Fluid}} ) \)**: Accounts for pressure-related forces on the fluid.
- **\( \frac{A_2}{A_t} \)**: The area ratio of the nozzle cross-section (\( A_2 \)) to the tank cross-section (\( A_t \)), indicating that the nozzle's diameter is much smaller.
#### Considerations for CO₂:
For part (2), it is required to use the same fundamental principles but with the properties relevant to CO₂.
### Conclusion:
The task emphasizes understanding fluid flow through a nozzle using basic principles of fluid dynamics, such as Bernoulli’s equation, considering different fluids and flow conditions.
Expert Solution
Step 1
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you

Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education

Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education

Control Systems Engineering
Mechanical Engineering
ISBN:
9781118170519
Author:
Norman S. Nise
Publisher:
WILEY

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning

Engineering Mechanics: Statics
Mechanical Engineering
ISBN:
9781118807330
Author:
James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:
WILEY