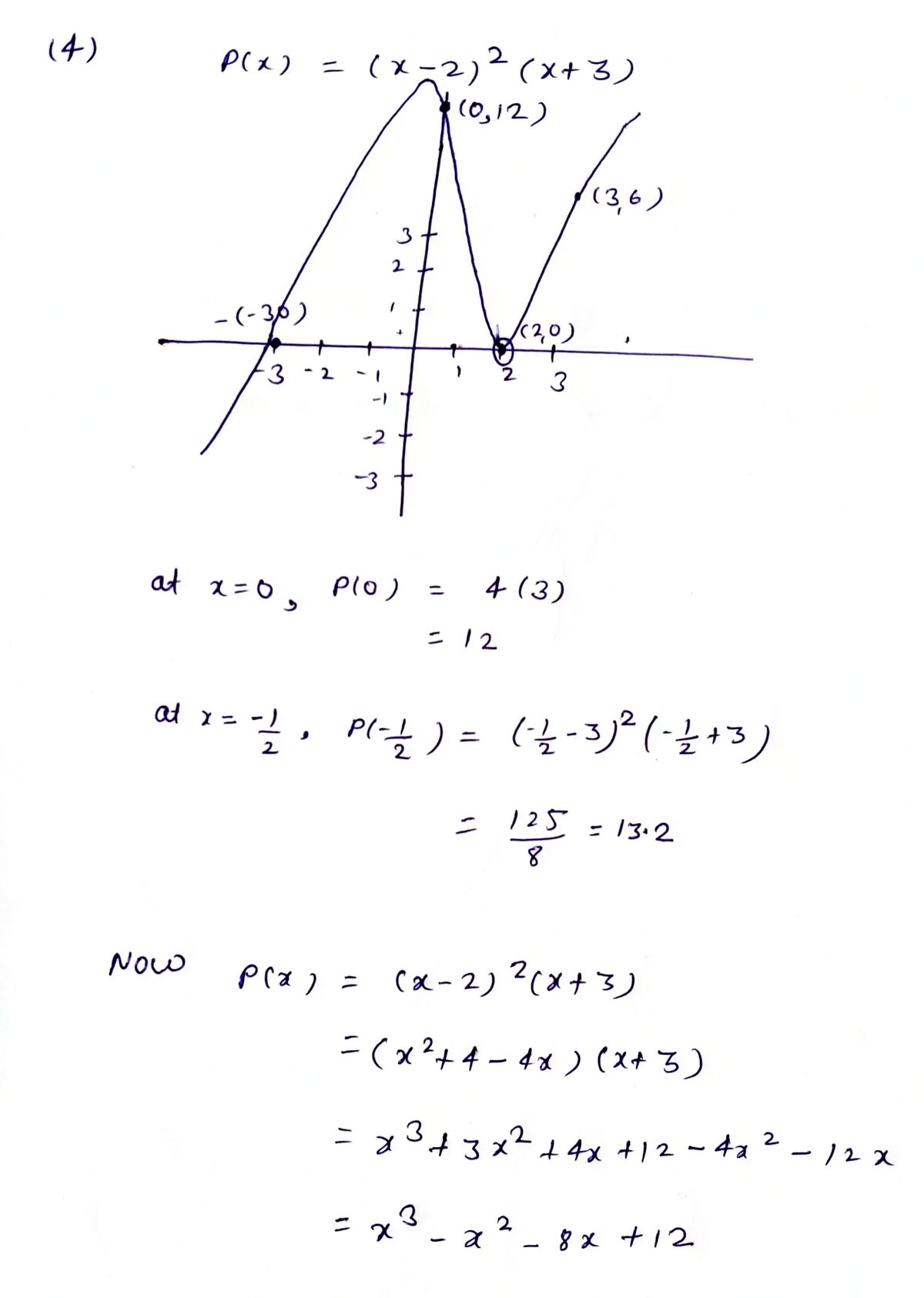
4) p(x) = (x-2)²(x+3) x²-x-4+x+3
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Can someone please help? Thank you.
![## Polynomial Analysis
### Problem 4:
\[ p(x) = (x-2)^2(x+3) \]
### Graph Explanation:
There is an empty coordinate graph, with labeled x and y axes, provided for plotting or visual analysis.
### Key Details:
- **Leading Term:** \( x^3 \) (derived from expanding the polynomial)
- **End Behavior:** As \( x \to \infty, p(x) \to \infty \) and as \( x \to -\infty, p(x) \to -\infty \), typical of an odd-degree polynomial with a positive leading coefficient.
- **Zeros of the Polynomial:**
- \( x = 2 \) with multiplicity 2 (the graph will touch the x-axis and turn around at this point).
- \( x = -3 \) with multiplicity 1 (the graph will cross the x-axis at this point).
### Multiplicity:
- **\( x = 2 \):** Multiplicity 2
- **\( x = -3 \):** Multiplicity 1
These characteristics of the polynomial determine the general shape and behavior of its graph. Analyzing the zeros and their multiplicities helps in sketching an accurate graph by indicating where and how the curve interacts with the x-axis.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Faad3bd42-2a78-4e81-96eb-d0945517a9ea%2Fcb340580-66d1-4593-8275-958b38374bcb%2Fzabaa9ko_processed.jpeg&w=3840&q=75)
Transcribed Image Text:## Polynomial Analysis
### Problem 4:
\[ p(x) = (x-2)^2(x+3) \]
### Graph Explanation:
There is an empty coordinate graph, with labeled x and y axes, provided for plotting or visual analysis.
### Key Details:
- **Leading Term:** \( x^3 \) (derived from expanding the polynomial)
- **End Behavior:** As \( x \to \infty, p(x) \to \infty \) and as \( x \to -\infty, p(x) \to -\infty \), typical of an odd-degree polynomial with a positive leading coefficient.
- **Zeros of the Polynomial:**
- \( x = 2 \) with multiplicity 2 (the graph will touch the x-axis and turn around at this point).
- \( x = -3 \) with multiplicity 1 (the graph will cross the x-axis at this point).
### Multiplicity:
- **\( x = 2 \):** Multiplicity 2
- **\( x = -3 \):** Multiplicity 1
These characteristics of the polynomial determine the general shape and behavior of its graph. Analyzing the zeros and their multiplicities helps in sketching an accurate graph by indicating where and how the curve interacts with the x-axis.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

