[4] Let X = C(0, 1; R)={@:[0,1]–→ R:0(;) is continuous} , with inner product (Aø().w() = fu(s)ø(s)ds . Consider the differential operator A: D(A)c X → X defined by A[@()](x)= g'(x), with domain D(A)= {@() e C' (0,1; R) : P(1) = 0} . (4a) Show that A is dissipative: (i.e., show that (A@(:),@())< 0 for all ø(-) e D(A)). (A9(), pO) = (4b) Could y =1 be an eigenvalue of A ? Give a reason for your answer. (4c) Let ø(x)= (x – 1) and w(x) = x² – x. Note both functions are in D(A) = {@() e C'(0,1; R): 9(1) = 0}: Compute: (Aø(), y(). (Aø(),w(O) =
[4] Let X = C(0, 1; R)={@:[0,1]–→ R:0(;) is continuous} , with inner product (Aø().w() = fu(s)ø(s)ds . Consider the differential operator A: D(A)c X → X defined by A[@()](x)= g'(x), with domain D(A)= {@() e C' (0,1; R) : P(1) = 0} . (4a) Show that A is dissipative: (i.e., show that (A@(:),@())< 0 for all ø(-) e D(A)). (A9(), pO) = (4b) Could y =1 be an eigenvalue of A ? Give a reason for your answer. (4c) Let ø(x)= (x – 1) and w(x) = x² – x. Note both functions are in D(A) = {@() e C'(0,1; R): 9(1) = 0}: Compute: (Aø(), y(). (Aø(),w(O) =
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![[4] Let X = C(0, 1; R)={@:[0,1]→ R : 9(-) is continuous} , with inner product
(A9(),y() = [y(s)ø(s)ds .
Consider the differential operator A:D(A)c X → X defined by A[9()](x) = g'(x),
with domain D(A)= {#(•) e C' (0,1; R): p(1) = 0} .
(4a) Show that A is dissipative:
(i.e., show that (Ap(:), p()) < 0 for all ø(-) e D(A)).
(Ap(),@() =
(4b) Could y = 1 be an eigenvalue of A? Give a reason for your answer.
(4c) Let ø(x)= (x-1) and w(x) = x² – x. Note both functions are in
D(A) = {@() e C' (0,1; R): ø(1) = 0} : Compute: (Ap(:), y ().
(Aø),wO) =](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F6baccc75-c439-41b7-9149-8921c6d5752c%2F11dc9714-a5f6-4099-a85b-09862f6ab6ae%2Fwepxaqc_processed.png&w=3840&q=75)
Transcribed Image Text:[4] Let X = C(0, 1; R)={@:[0,1]→ R : 9(-) is continuous} , with inner product
(A9(),y() = [y(s)ø(s)ds .
Consider the differential operator A:D(A)c X → X defined by A[9()](x) = g'(x),
with domain D(A)= {#(•) e C' (0,1; R): p(1) = 0} .
(4a) Show that A is dissipative:
(i.e., show that (Ap(:), p()) < 0 for all ø(-) e D(A)).
(Ap(),@() =
(4b) Could y = 1 be an eigenvalue of A? Give a reason for your answer.
(4c) Let ø(x)= (x-1) and w(x) = x² – x. Note both functions are in
D(A) = {@() e C' (0,1; R): ø(1) = 0} : Compute: (Ap(:), y ().
(Aø),wO) =
Expert Solution
Step 1
(a) Consider the provided question,
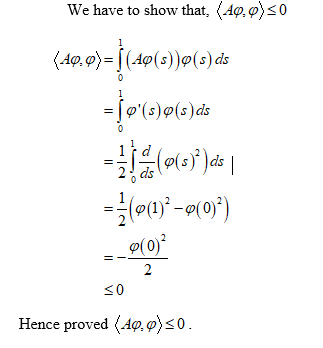
Step 2

Step by step
Solved in 3 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

