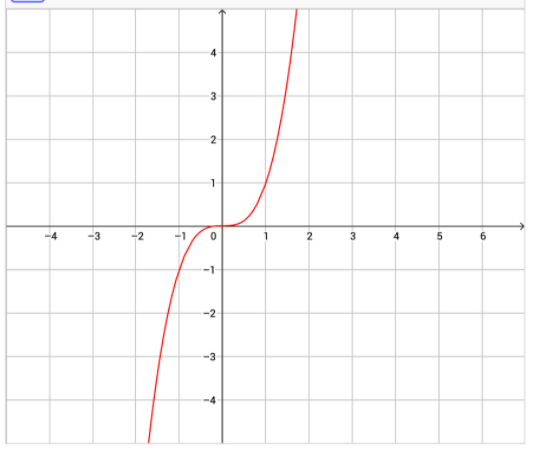
This graph displays the function \( y = x^3 \), a cubic function known for its distinct shape. The graph is plotted on a Cartesian coordinate system, featuring both x and y-axes:- **Axes**: - The x-axis ranges from -4 to 6. - The y-axis ranges from -4 to 5.- **Function Behavior**: - For negative values of x, the function has negative values, extending downward to the left. - As x approaches zero from the left, the function increases sharply. - At \( x = 0 \), the function passes through the origin (0,0). - For positive values of x, the function values rise sharply, showcasing an increasing trend as x continues to increase.- **Symmetry & Shape**: - The curve is symmetric with respect to the origin, exhibiting odd symmetry. - It illustrates a smooth curve without any breaks or corners, characteristic of polynomial functions.This cubic curve is a fundamental example of polynomial graphs, highlighting key properties such as end behavior, extremas, and intercepts, useful for both theoretical and applied mathematical studies. ## Task: Calculate the Value of a Function### Problem Statement:Find \( f(2) \)\( f(2) = \)---### Instructions:1. **Input Field**: Enter your answer in the provided space.2. **Submit Answer Button**: Click this button to check your answer.3. **Error Message**: If you see "Unable to understand formula," review your input for any mistakes.4. **Tries Information**: You have attempted this problem 1 out of 99 possible tries.5. **Previous Tries**: Click this link to review past attempts.Use these instructions to complete the calculation and submit your answer for evaluation.

Answered: Image /qna-images/answer/24d153c9-64aa-4797-955d-9b8314a419a7.jpg

Answered: -4 2- -3 -2 -1 1 2 4 5 --1 --2 --3 -4…

-4 2- -3 -2 -1 1 2 4 5 --1 --2 --3 -4 3. 3.

6th Edition

ISBN:9780134463216

Author:Robert F. Blitzer

Publisher:Robert F. Blitzer

ChapterP: Prerequisites: Fundamental Concepts Of Algebra

Section: Chapter Questions

Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...

Similar questions

Which graph represents a function? -3 -2 -1 1 2 3 -1 -2 -3 3. 2 1 -3 3 -1 -1 1 -2 -3
3x + 4y = 8 -2 4 -2 -41 -2 -2 C 1x
-1 -3 -1 -21 A = -5 -15 -2 11 3 2 -6 -5 -4 -5
Simplify, 5. (16+2)2-2-(8-5)² 5-(16+2)2-2-(8-5)² = (
6 1/3 − 2 3/4 Express answer as a reduced mixed number.
3[9 / (-3) } + (-3 - (-8)]
( 4 + -9) ÷ [ -10 - (-5)] • (-2)
-3 (3x-2) 10. Jo 2+2х+17