3. Use logical equivalences to simplify each one of following a) ((PA¬Q) V (PAQ)) ^Q (b)-((-p^g)v(p^-q))v (p^q)
3. Use logical equivalences to simplify each one of following a) ((PA¬Q) V (PAQ)) ^Q (b)-((-p^g)v(p^-q))v (p^q)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Need the solution to number 3, please explain process to solution. Thank you

Transcribed Image Text:1. Apply a truth table to show each conclusion of following:
(a) ~(-p) = p
(b) ~(pVq) = (~p) ^ (~q)
2. Write down the converse, inverse and contra-positive of each of the following statements:
(a) For any real number x, if x >4, then x² > 16.
(b) If both a and b are integers, then their product ab is an integer.
3. Use logical equivalences to simplify each one of following
a) ((PA¬Q) V (PAQ)) ^Q (b)-((-p^q) v (p^-q)) v (p^q)
4. Negating the following statements:
(a) V primes p, p is odd.
(b) 3 a triangle T such that the sum of the angles equals 200°.
(c) For every square x there is a triangle y such that x and y have different colors.
(d) There exists a triangle y such that for every square x, x and y have different colors.
(e) V people p, if p is blond then p has blue eyes.
5. Construct a truth table to determine whether or not the argument is valid
(a)
(b)
pv (q vr)
יזר
pv q
p→qv (¬r)
q→ p^r
:p →r
6. Prove that
(a) 9n² + 3n-2 is even for any integer n.
(b) For all integers mann, m+nand m-nare either both odd or both even.
(c) There are real numbers such that √a + b = √a + √b.
(d) For all integers, if n is odd then n²is odd.
7. Show that the following statements are false:
(a) There is an integer n such that 2n² - 5n + 2 is a prime.
(b) If m and n are any two positive integers then mn > m + n.
Expert Solution
Step 1: Recall some logical equivalence.
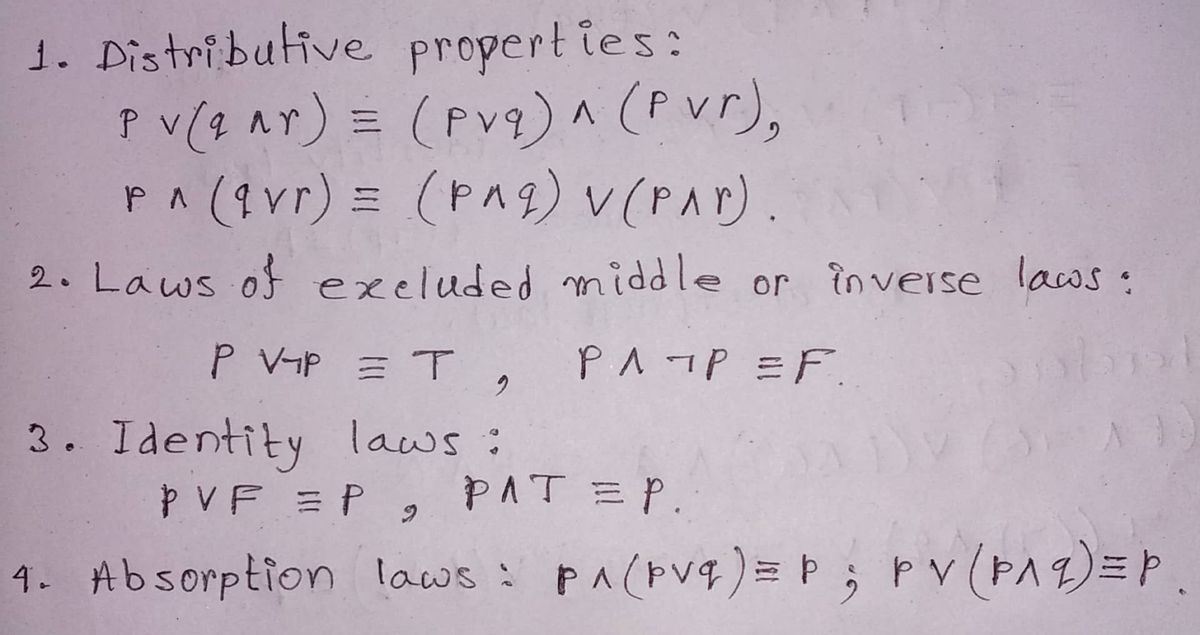
Step by step
Solved in 3 steps with 4 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

