Homework Help is Here – Start Your Trial Now!
Math
Calculus
3. Let i, j, k denote the unit vectors along the three coordinate axes. Let v(t) = ti + sintj + costk and w(t) = 3ti + 2k. (a) Compute (v.w)'(t) directly and check your answer by using the product rule (for the dot product, stated in the class). Note that the dot above, is the dot product of vectors and' denotes the derivative. (b) Compute (vx w)'(t) directly and check your answer by using the product rule (for the cross product, again stated in the class). Note that the x above, is the cross product of vectors.

3. Let i, j, k denote the unit vectors along the three coordinate axes. Let v(t) = ti + sintj + costk and w(t) = 3ti + 2k. (a) Compute (v.w)'(t) directly and check your answer by using the product rule (for the dot product, stated in the class). Note that the dot above, is the dot product of vectors and' denotes the derivative. (b) Compute (vx w)'(t) directly and check your answer by using the product rule (for the cross product, again stated in the class). Note that the x above, is the cross product of vectors.

Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
See similar textbooks
icon
Related questions
Question
3. Let i, j, k denote the unit vectors along the three coordinate axes. Let v(t) = ti+ sintj + costk and w(t) = 3ti + 2k. (a) Compute (v.w)' (t) directly and check your answer by using the product rule (for the dot product, stated in the class). Note that the dot above, is the dot product of vectors and denotes the derivative. (b) Compute (v x w)'(t) directly and check your answer by using the product rule (for the cross product, again stated in the class). Note that the x above, is the cross product of vectors.
Transcribed Image Text:3. Let i, j, k denote the unit vectors along the three coordinate axes. Let v(t) = ti+ sintj + costk and w(t) = 3ti + 2k. (a) Compute (v.w)' (t) directly and check your answer by using the product rule (for the dot product, stated in the class). Note that the dot above, is the dot product of vectors and denotes the derivative. (b) Compute (v x w)'(t) directly and check your answer by using the product rule (for the cross product, again stated in the class). Note that the x above, is the cross product of vectors.
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 5 steps

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

can you show how do you calculate for these two parts?

=(i + (cos t)j + (− sin t)k) × ((3t)i + 2k) + ((t)i + (sin t)j + (cos t)) × (3i + 0k) i j ki j k cos tsin t+t sin t 1 3t 0 2 3 0 0 =(2 cos t)i + (−2 − 3t sin t)j + (−3t cos t)k + 0i+ (3 cos t)j + (−3 sin t)k cos t
Transcribed Image Text:=(i + (cos t)j + (− sin t)k) × ((3t)i + 2k) + ((t)i + (sin t)j + (cos t)) × (3i + 0k) i j ki j k cos tsin t+t sin t 1 3t 0 2 3 0 0 =(2 cos t)i + (−2 − 3t sin t)j + (−3t cos t)k + 0i+ (3 cos t)j + (−3 sin t)k cos t
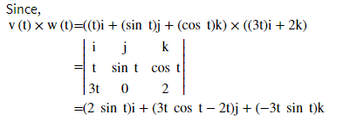
Since, v (t) x w (t)=((t)i + (sin t)j + (cos t)k) x ((3t)i + 2k) k i t cos t 3t 0 2 =(2 sin t)i + (3t cos t − 2t)j + (−3t sin t)k j sint
Transcribed Image Text:Since, v (t) x w (t)=((t)i + (sin t)j + (cos t)k) x ((3t)i + 2k) k i t cos t 3t 0 2 =(2 sin t)i + (3t cos t − 2t)j + (−3t sin t)k j sint
Solution
Bartleby Expert
SEE SOLUTION
Recommended textbooks for you
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman
Precalculus
Precalculus
Calculus
ISBN:
9780135189405
Author:
Michael Sullivan
Publisher:
PEARSON
Calculus: Early Transcendental Functions
Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS