3. Assume that f : R → R is such that |f(x) – f(y)| < A\x – y| for all x, y E R and some A E (0, 1). Pick xo E R arbitrarily, and construct a sequence (xn) as follows: xn+1 f(xn) for n > 0. (a) Prove that |æn+1 – Xn] < \|xn – xn-1| for all n > 1. (b) Prove that |æn+1– Xn[ < \"|x1 – xo] for all n > 1. (c) Prove that (xn) is convergent. (d) Let x* lim xn. Prove that f(x*) = x*. ||
3. Assume that f : R → R is such that |f(x) – f(y)| < A\x – y| for all x, y E R and some A E (0, 1). Pick xo E R arbitrarily, and construct a sequence (xn) as follows: xn+1 f(xn) for n > 0. (a) Prove that |æn+1 – Xn] < \|xn – xn-1| for all n > 1. (b) Prove that |æn+1– Xn[ < \"|x1 – xo] for all n > 1. (c) Prove that (xn) is convergent. (d) Let x* lim xn. Prove that f(x*) = x*. ||
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![3. Assume that f : R → R is such that |f(x) – f (y)| < A|x – y| for all x, y E R
and some A E (0,1). Pick xo E R arbitrarily, and construct a sequence (xn)
as follows: n+1
f (xn) for n > 0.
(a) Prove that |Xn+1 – Xn[ < A|xn
Xn-1| for all n > 1.
(b) Prove that |xn+1 – Xn| < \"|x1 – xo] for all n > 1.
(c) Prove that (xn) is convergent.
(d) Let x*
lim xn. Prove that f(x*) = x*.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F7fd47556-f3ce-4f39-818d-be563d9523c8%2F7d48a182-9626-43ba-9f05-bc79cf8ee5aa%2Fy5f7pnl_processed.jpeg&w=3840&q=75)
Transcribed Image Text:3. Assume that f : R → R is such that |f(x) – f (y)| < A|x – y| for all x, y E R
and some A E (0,1). Pick xo E R arbitrarily, and construct a sequence (xn)
as follows: n+1
f (xn) for n > 0.
(a) Prove that |Xn+1 – Xn[ < A|xn
Xn-1| for all n > 1.
(b) Prove that |xn+1 – Xn| < \"|x1 – xo] for all n > 1.
(c) Prove that (xn) is convergent.
(d) Let x*
lim xn. Prove that f(x*) = x*.
Expert Solution
Step 1
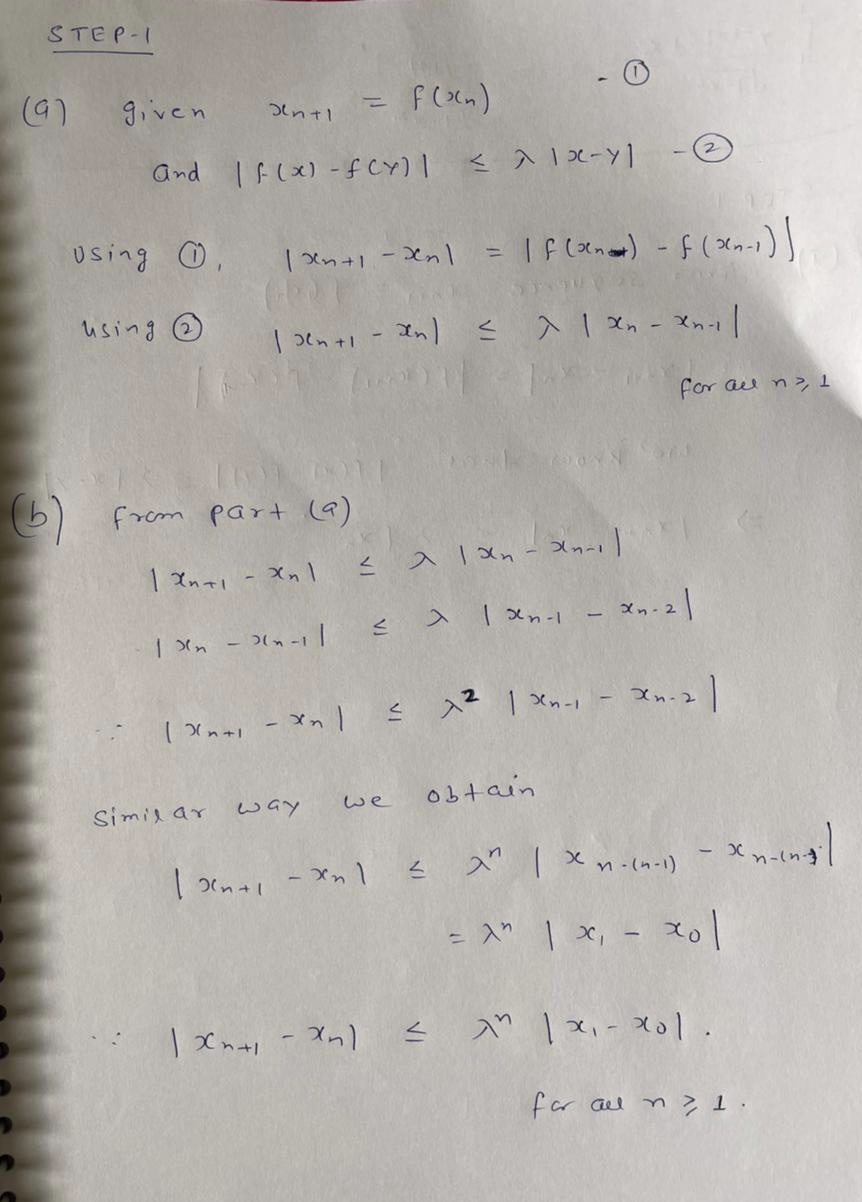
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

