3) (Treat as an "energy" problem) While exploring an abandoned barn, Lobster got stuck in a crate down a shaft. Luckily the (massless, frictionless) pulley system is intact. Frog's plan to rescue its friend consists of jumping up to the end of the rope, which it can just barely reach, and using its weight to hoist Lobster up. Unfortunately, h
3) (Treat as an "energy" problem) While exploring an abandoned barn, Lobster got stuck in a crate down a shaft. Luckily the (massless, frictionless) pulley system is intact. Frog's plan to rescue its friend consists of jumping up to the end of the rope, which it can just barely reach, and using its weight to hoist Lobster up. Unfortunately, h
Related questions
Question
Hello,
Can someone please show how to solve parts a b and c please?
Thank you

Transcribed Image Text:**Problem 3: Energy and Motion**
**Scenario:**
While exploring an abandoned barn, Lobster got stuck in a crate down a shaft. Luckily, the massless, frictionless pulley system is intact. Frog’s plan is to rescue its friend by jumping up to the end of the rope and using its weight to hoist Lobster up. Unfortunately, \( h < D \), and \( m_F < m_L \). However, Frog has unlimited amounts of candy to snack on, which helps in the rescue mission.
**Treat as a 1D problem:**
**Questions:**
(a) **Initial Scenario:** If Frog jumps up and holds onto the loose end of the rope without eating any candy, describe what happens next using words.
(b) **Complete Plan Description:** In your own words, explain a complete, successful plan. Describe the motion(s) and a suitable system for each motion.
(c) **Energy Analysis:** Determine the potential and kinetic energies of both Frog and Lobster just before the moment Frog returns to the ledge.
(d) **Candy Requirement:** How many pieces of candy (each with mass \( m \)) does Frog need to eat to bring Lobster up to the upper floor level?
(e) **Plan Feasibility:** Will this plan work for all values of \( h \)? Provide a Yes/No answer and explanation.
**Diagram Explanation:**
- A pulley system with Frog on one side and Lobster in a crate on the other.
- Frog is on a ledge and needs to jump a height \( h \).
- The Lobster is in a crate at a depth \( D \) below.
- \( m_F \) denotes the mass of the Frog, \( m_L \) is the mass of the Lobster, and \( m \) is the mass of each candy piece.
- The crate is visually marked with a dashed line indicating Lobster’s confinement.
This educational content focuses on dynamics and energy, emphasizing practical problem-solving using physics concepts such as energy conservation and force balance.
Expert Solution
Step 1
a) mass of the frog=
mass of the crate together with mass of the lobster
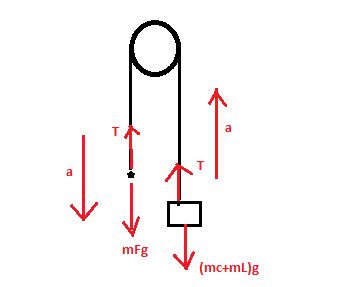
When the mass of the frog attaches itself to the end of the rope it will pull down the system rope with a tension T. The tension T will also help pull the joint mass of the crate and the lobster to pull it in the upward direction.
Since the mass of frog is very much less than the mass of the crate, it will tend to move crate in the upward direction slightly but not wholly.
b) For the motion to be successful, we should use the free body diagram:
Step by step
Solved in 4 steps with 1 images
