suppose that function f is defined as followsGraph the function F ## Graphing a Piecewise-Defined Function: Problem Type 1### Function DefinitionSuppose that the function $ f $ is defined as follows:\[f(x) = \begin{cases} -3 & \text{if } -2 \leq x < -1 \\-2 & \text{if } -1 \leq x < 0 \\-1 & \text{if } 0 \leq x < 1 \\0 & \text{if } 1 \leq x < 2 \end{cases}\]### Graph the Function $ f $Below is a visual representation of the function $ f(x) $ on a Cartesian plane.#### Explanation of the Graph- **Interval $[-2, -1)$**: - The function value is $ -3 $ for $ x $ in the range $[-2, -1)$. - This is plotted as a horizontal line at $ y = -3 $ from $ x = -2 $ to $ x = -1 $, with an open circle at $ x = -1 $ indicating that the endpoint is not included. - **Interval $[-1, 0)$**: - The function value is $ -2 $ for $ x $ in the range $[-1, 0)$. - This is plotted as a horizontal line at $ y = -2 $ from $ x = -1 $ to $ x = 0 $, also with an open circle at $ x = 0 $. - **Interval $[0, 1)$**: - The function value is $ -1 $ for $ x $ in the range $[0, 1)$. - This is plotted as a horizontal line at $ y = -1 $ from $ x = 0 $ to $ x = 1 $, with an open circle at $ x = 1 $. - **Interval $[1, 2)$**: - The function value is $ 0 $ for $ x $ in the range $[1, 2)$. - This is plotted as a horizontal line at $ y = 0 $ from $ x = 1 $ to $ x = 2 $, again with an open circle

Name: suppose that function f is defined as followsGraph the function F ## G
Uploaded: 2024-03-20T06:47:22.000Z
Channel: Bartleby
Description: suppose that function f is defined as followsGraph the function F ## Graphing a Piecewise-Defined Function: Problem Type 1### Function DefinitionSuppose that the function $ f $ is defined as follows:\[f(x) = \begin{cases} -3 & \text{if } -2 \leq x

Answered: -3 if – 2

Algebra and Trigonometry (6th Edition)

6th Edition

ISBN:9780134463216

Author:Robert F. Blitzer

Publisher:Robert F. Blitzer

ChapterP: Prerequisites: Fundamental Concepts Of Algebra

Section: Chapter Questions

Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...

See similar textbooks

Related questions

Topic Video

Question

100%

suppose that function f is defined as follows

Graph the function F

## Graphing a Piecewise-Defined Function: Problem Type 1

### Function Definition
Suppose that the function $ f $ is defined as follows:
\[
f(x) = \begin{cases}
-3 & \text{if } -2 \leq x < -1 \\
-2 & \text{if } -1 \leq x < 0 \\
-1 & \text{if } 0 \leq x < 1 \\
0 & \text{if } 1 \leq x < 2
\end{cases}
\]

### Graph the Function $ f $
Below is a visual representation of the function $ f(x) $ on a Cartesian plane.

#### Explanation of the Graph
- **Interval $[-2, -1)$**:
- The function value is $ -3 $ for $ x $ in the range $[-2, -1)$.
- This is plotted as a horizontal line at $ y = -3 $ from $ x = -2 $ to $ x = -1 $, with an open circle at $ x = -1 $ indicating that the endpoint is not included.

- **Interval $[-1, 0)$**:
- The function value is $ -2 $ for $ x $ in the range $[-1, 0)$.
- This is plotted as a horizontal line at $ y = -2 $ from $ x = -1 $ to $ x = 0 $, also with an open circle at $ x = 0 $.

- **Interval $[0, 1)$**:
- The function value is $ -1 $ for $ x $ in the range $[0, 1)$.
- This is plotted as a horizontal line at $ y = -1 $ from $ x = 0 $ to $ x = 1 $, with an open circle at $ x = 1 $.

- **Interval $[1, 2)$**:
- The function value is $ 0 $ for $ x $ in the range $[1, 2)$.
- This is plotted as a horizontal line at $ y = 0 $ from $ x = 1 $ to $ x = 2 $, again with an open circle

Expert Solution

Step 1

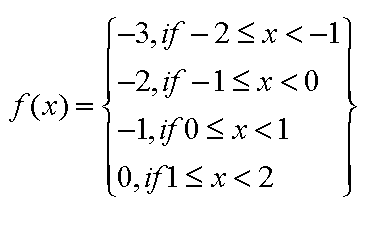
To graph piecewise function make a table for each function as per the given interval

Step 2

First function is f(x)=-3 , interval is from x= -2 to -1

Pick x that are end point of the given interval

While graphing use open circle for < symbol and closed interval for <= symbol

x	y=-3
-2	-3
-1	-3

Step 3

First function is f(x)=-2 , interval is from x= -1 to 0

Pick x that are end point of the given interval

x	y=-2
-1	-2
0	-2

Step by step

Solved in 6 steps with 2 images

Knowledge Booster

$Rules of Differentiation$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.

Similar questions