. Determine if valid or invalid. Using Rules of Inference. 28. If you play golf during a thunderstorm, you’ll get hit by lightning. You didn’t get hit by lightning. Therefore, you didn’t play golf during a thunderstorm.
. Determine if valid or invalid. Using Rules of Inference. 28. If you play golf during a thunderstorm, you’ll get hit by lightning. You didn’t get hit by lightning. Therefore, you didn’t play golf during a thunderstorm.
Computer Networking: A Top-Down Approach (7th Edition)
7th Edition
ISBN:9780133594140
Author:James Kurose, Keith Ross
Publisher:James Kurose, Keith Ross
Chapter1: Computer Networks And The Internet
Section: Chapter Questions
Problem R1RQ: What is the difference between a host and an end system? List several different types of end...
Related questions
Question
D. Determine if valid or invalid. Using Rules of Inference.
28. If you play golf during a thunderstorm, you’ll get hit by lightning. You didn’t get hit by lightning. Therefore, you didn’t play golf during a thunderstorm.

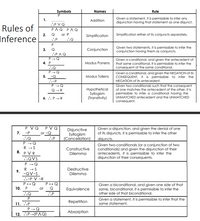
Transcribed Image Text:Symbols
Names
Rule
Given a statement, it is permissible to infer any
disjunction having that statement as one disjunct.
1.
Addition
..P VQ
Rules of
PAQ PAQ
2.
Q
or P
Simplification
Simplification either of its conjuncts separately.
Inference
..P
..Q
Given two statements, it is permissible to infer the
conjunction having them as conjuncts.
3.
Q
Conjunction
..PAQ
P- Q
Given a conditional, and given the antecedent of
4. P
Modus Ponens
that same conditional, it is permissible to infer the
consequent of the same conditional.
P.
Given a conditional, and given the NEGATION of its
CONSEQUENT, it is permissible to infer the
NEGATION of its antecedent.
Given two conditionals such that the consequent
of one matches the antecedent of the other, it is
permissible to infer a conditional having the
UNMATCHED antecedent and the UNMATCHED
5.
Modus Tollens
P - Q
Hypothetical
Syllogism
(Transitivity)
Q-R
6. .. P-R
consequent.
P VQ
PVQ
Disjunctive
Sylogism
(Cancellation) disjuncts.
Given a disjunction, and given the denial of one
of its disjuncts, it is permissible to infer the other
7. -P
or -Q
..Q
.P
P - Q
Given two conditionals (or a conjunction of two
conditionals) and given the disjunction of their
antecedents, it is permissible to infer the
disjunction of their consequents.
8. PVR
Constructive
Dilemma
.QVS
P - Q
R -S
9.
-QV-S
Destructive
Dilemma
..-P V -R
P+Q
P+Q
Given a biconditional, and given one side of that
same, biconditional, it is permissible to infer the
other side of that biconditional.
10. Р
or
Q
Equivalence
.Q
P
Given a statement, it is permissible to infer that the
Repetition
11. ..P
P → Q
12. ..Р—(РЛQ)
same statement.
Absorption
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Yes by definition you are correct. But I need help by analyzing whether the given statement is valid or invalid using the rules of inference. Thank you if ever you will help me correctly this time.
D. Determine if valid or invalid. Using Rules of Inference.
28. If you play golf during a thunderstorm, you’ll get hit by lightning. You didn’t get hit by lightning. Therefore, you didn’t play golf during a thunderstorm.
Transcribed Image Text:Symbols
Names
Rule
Given a statement, it is permissible to infer any
disjunction having that statement as one disjunct.
1.
Addition
..P VQ
Rules of
PAQ PAQ
2.
Q
or P
Simplification
Simplification either of its conjuncts separately.
Inference
..P
..Q
Given two statements, it is permissible to infer the
conjunction having them as conjuncts.
3.
Q
Conjunction
..PAQ
P- Q
Given a conditional, and given the antecedent of
4. P
Modus Ponens
that same conditional, it is permissible to infer the
consequent of the same conditional.
P.
Given a conditional, and given the NEGATION of its
CONSEQUENT, it is permissible to infer the
NEGATION of its antecedent.
Given two conditionals such that the consequent
of one matches the antecedent of the other, it is
permissible to infer a conditional having the
UNMATCHED antecedent and the UNMATCHED
5.
Modus Tollens
P - Q
Hypothetical
Syllogism
(Transitivity)
Q-R
6. .. P-R
consequent.
P VQ
PVQ
Disjunctive
Sylogism
(Cancellation) disjuncts.
Given a disjunction, and given the denial of one
of its disjuncts, it is permissible to infer the other
7. -P
or -Q
..Q
.P
P - Q
Given two conditionals (or a conjunction of two
conditionals) and given the disjunction of their
antecedents, it is permissible to infer the
disjunction of their consequents.
8. PVR
Constructive
Dilemma
.QVS
P - Q
R -S
9.
-QV-S
Destructive
Dilemma
..-P V -R
P+Q
P+Q
Given a biconditional, and given one side of that
same, biconditional, it is permissible to infer the
other side of that biconditional.
10. Р
or
Q
Equivalence
.Q
P
Given a statement, it is permissible to infer that the
Repetition
11. ..P
P → Q
12. ..Р—(РЛQ)
same statement.
Absorption
Solution
Recommended textbooks for you

Computer Networking: A Top-Down Approach (7th Edi…
Computer Engineering
ISBN:
9780133594140
Author:
James Kurose, Keith Ross
Publisher:
PEARSON

Computer Organization and Design MIPS Edition, Fi…
Computer Engineering
ISBN:
9780124077263
Author:
David A. Patterson, John L. Hennessy
Publisher:
Elsevier Science

Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:
9781337569330
Author:
Jill West, Tamara Dean, Jean Andrews
Publisher:
Cengage Learning

Computer Networking: A Top-Down Approach (7th Edi…
Computer Engineering
ISBN:
9780133594140
Author:
James Kurose, Keith Ross
Publisher:
PEARSON

Computer Organization and Design MIPS Edition, Fi…
Computer Engineering
ISBN:
9780124077263
Author:
David A. Patterson, John L. Hennessy
Publisher:
Elsevier Science

Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:
9781337569330
Author:
Jill West, Tamara Dean, Jean Andrews
Publisher:
Cengage Learning

Concepts of Database Management
Computer Engineering
ISBN:
9781337093422
Author:
Joy L. Starks, Philip J. Pratt, Mary Z. Last
Publisher:
Cengage Learning

Prelude to Programming
Computer Engineering
ISBN:
9780133750423
Author:
VENIT, Stewart
Publisher:
Pearson Education

Sc Business Data Communications and Networking, T…
Computer Engineering
ISBN:
9781119368830
Author:
FITZGERALD
Publisher:
WILEY