Certainly! Here is the transcription of the image text suitable for an educational website:---12. Take a moment to understand the Lagrange multipliers method for finding min/max on a surface $ f(x, y, z) $ subject to a constraint $ g(x, y, z) = 0 $. Geometrically speaking, what does it mean for $ \nabla f = \lambda \nabla g $? Why are the candidates for minimums & maximums exactly the points that satisfy this equation?---The text invites readers to explore how the method of Lagrange multipliers helps in identifying extrema (minimums and maximums) of a function with a constraint. It poses a geometric interpretation question about the condition $ \nabla f = \lambda \nabla g $, where the gradients of the functions $ f $ and $ g $ are scalar multiples of each other, indicating potential points of extrema that lie on the constrained surface.

Answered: 2. Take a moment to understand the…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Question

Certainly! Here is the transcription of the image text suitable for an educational website:

---

12. Take a moment to understand the Lagrange multipliers method for finding min/max on a surface $ f(x, y, z) $ subject to a constraint $ g(x, y, z) = 0 $. Geometrically speaking, what does it mean for $ \nabla f = \lambda \nabla g $? Why are the candidates for minimums & maximums exactly the points that satisfy this equation?

---

The text invites readers to explore how the method of Lagrange multipliers helps in identifying extrema (minimums and maximums) of a function with a constraint. It poses a geometric interpretation question about the condition $ \nabla f = \lambda \nabla g $, where the gradients of the functions $ f $ and $ g $ are scalar multiples of each other, indicating potential points of extrema that lie on the constrained surface.

Expert Solution

Step 1

Suppose we want to find the maximum of a function $f (x, y) = x y$ subject to a constraint $g (x, y) = \frac{x^{2}}{9} + \frac{y^{2}}{4} - 1$ .

To see how Lagrange multipliers work, look at the following graph:

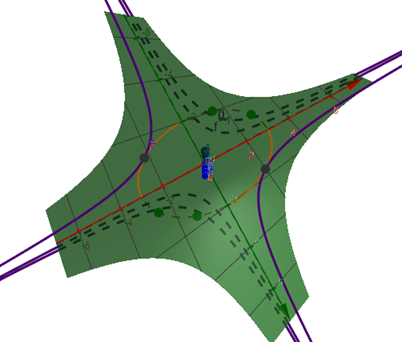
Figure 1

The graph shows the function f from above along with constraint g = c and some level curves of f. The constraint is nothing but a plane that cuts through the function f.

The constraint g is an ellipse on xy-plane projected on to the surface f. The goal here is to find the maximum value of f without moving outside the elliptic boundary.