2. Exercise 7 in §0.1 Let f : A B be a surjective map of sets. Prove that the relation a-bif and only if f(a) = f(b) is an equivalence relation whose equivalence classes are the fibers of f. Hint: Use Proposition 2 in the textbook.
2. Exercise 7 in §0.1 Let f : A B be a surjective map of sets. Prove that the relation a-bif and only if f(a) = f(b) is an equivalence relation whose equivalence classes are the fibers of f. Hint: Use Proposition 2 in the textbook.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:Homework Assignment 1
МАTH 541
This homework assignment corresponds with material covered through January 29, Sections 0.1, 0.2, 0.3
8 1.1 in Dummit & Foote Abstract Algebra 3rd Ed. Please write the problems and solutions on separate
sheets of paper. The calculations, erplanations, and proofs should be in complete coherent and logical
sentences. This assignment is due on Thursday, February 4 at 11:59pm in Canvas as a .pdf file.
1. Exercise 5 in 80.1. Determine whether the following functions f are well defined:
(a) f:Q→ Z defined by f(a/b) = a.
(b) f:Q→Q defined by f(a/b) = a² /b°.
2. Exercise 7 in $0.1 Let f : A → B be a surjective map of sets. Prove that the relation
a - b if and only if f(a) = f(b)
is an equivalence relation whose equivalence classes are the fibers of f.
Hint: Use Proposition 2 in the textbook.
3. Let n > 2. For any a, b e Z, proof that n | (b – a) if and only if a and b have the same remainder
when divided by n. Conclude that a = b (mod n) if and only if a and b have the same remainder
when divided by n.
4. Exercise 11 in 80.3 Prove that if ā, b € (Z/nZ)*, then ā - be (Z/nZ) *.
5. Exercise 6 in §1.1. Determine which of the following sets are groups under addition. Explain why or
why not.
(a) the set of rational numbers (including 0 = 0/1) in lowest terms whose denominators are odd.
(b) the set of rational numbers in lowest terms whose denominators are even together with 0.
(c) the set of rational numbers of absolute value < 1.
(d) the set of rational numbers of absolute value >1 together with 0.
(e) the set of rational numbers with denominators equal to 1 or 2.
(f) the set of rational numbers with denominators equal to 1, 2, or 3.
{(: ) -
6. Prove that GLn(R) =
: ad – bc + C
C Mat2x2(R) (called the general linear group of
degree 2) is a group under matrix multiplication. Does your argument work for any degree n?
Hint: Use the property det(AB) = det A · det B. for all A, B E Matnxn(R).
7. Is the set U =
: ad – bc = 1
C Mat2x2 (R) a group under matrix multiplication?
8. Exercise 5 in §1.1. Prove for all n > 1 that Z/nZ is not a group under multiplication of residue
classes.
Expert Solution
Step 1
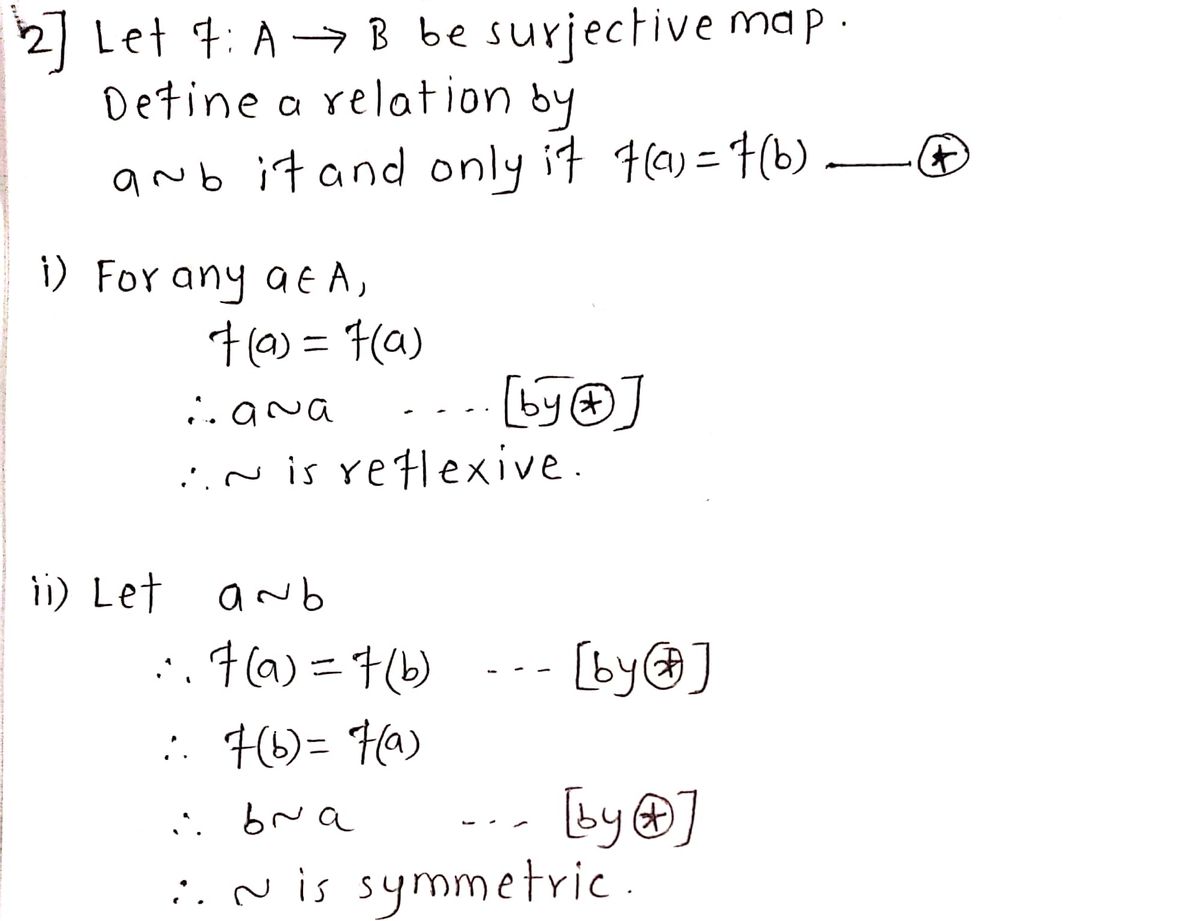
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

