[2] Water in a U-tube is held at unequal heights by placing a thumb over one end. The diameter of the tube is 1.5 cm and the total length of the water column is 8 cm, top right to top left. The initial height difference is h as shown in the figure. (a) if we set y=0 at the equilibrium height for the water, what is the value of y, =y (t= 0) for the right column? (b) When the thumb is removed, what happens during the next several seconds? (c) Set up Newton's 2 law for the water column starting with the pressures. (d) Compare the result with the oscillator equation and determine the expression for the angular frequency @. (e) Student I. Maslow Starter began the data collection 0.5[s] after the thumb was removed. The height y at that time was 0.8yo. Determine the velocity of the water column at that time in terms of g, p & yo- (f) Use your values of yo & the initial velocity v, to determine the amplitudes A & B in y = Acos (ot)+ B sin(@t) and, from those, find the amplitude D and phase shift ô in y =D cos( at + 8) (9) The amplitude of the motion decreases by 10% per period. Determine the damping constant B in e", the damping coefficient, b in F = -bv and the resonance frequency of %3D the damped oscillator.
[2] Water in a U-tube is held at unequal heights by placing a thumb over one end. The diameter of the tube is 1.5 cm and the total length of the water column is 8 cm, top right to top left. The initial height difference is h as shown in the figure. (a) if we set y=0 at the equilibrium height for the water, what is the value of y, =y (t= 0) for the right column? (b) When the thumb is removed, what happens during the next several seconds? (c) Set up Newton's 2 law for the water column starting with the pressures. (d) Compare the result with the oscillator equation and determine the expression for the angular frequency @. (e) Student I. Maslow Starter began the data collection 0.5[s] after the thumb was removed. The height y at that time was 0.8yo. Determine the velocity of the water column at that time in terms of g, p & yo- (f) Use your values of yo & the initial velocity v, to determine the amplitudes A & B in y = Acos (ot)+ B sin(@t) and, from those, find the amplitude D and phase shift ô in y =D cos( at + 8) (9) The amplitude of the motion decreases by 10% per period. Determine the damping constant B in e", the damping coefficient, b in F = -bv and the resonance frequency of %3D the damped oscillator.
Related questions
Question
I got sqrt(g/4) as my omega from part d. However, I don't how to proceed from there to answer part e,f and g
![[2] Water in a U-tube is held at unequal heights by placing a thumb over one end. The
diameter of the tube is 1.5 cm and the total length of the water column is 8 cm, top right
to top left.
The initial height difference is h as shown in the figure.
(a) if we set y=0 at the equilibrium height for the water, what is the
value of y, = y (t = 0) for the right column?
(b) When the thumb is removed, what happens during the next several
seconds?
(c) Set up Newton's 2nd law for the water column starting with the pressures.
(d) Compare the result with the oscillator equation and determine the expression for the
angular frequency .
(e) Student I. Maslow Starter began the data collection 0.5[s] after the thumb was
removed. The height y at that time was 0.8yo. Determine the velocity of the water column
at that time in terms of g. p & yo.
(f) Use your values of yo & the initial velocity v, to determine the amplitudes A & B in
y = Acos (at) + B sin(@t) and, from those, find the amplitude D and phase shift d in
y = D cos( ot + 8)
(9) The amplitude of the motion decreases by 10% per period. Determine the damping
constant B in e, the damping coefficient, b in F = -by and the resonance frequency of
the damped oscillator.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F9de2b0ed-01a2-4a8a-9b30-8cd619de91d2%2Fff58b8d9-df9a-491a-9a12-8fcd762ee95e%2F47xwc3m_processed.png&w=3840&q=75)
Transcribed Image Text:[2] Water in a U-tube is held at unequal heights by placing a thumb over one end. The
diameter of the tube is 1.5 cm and the total length of the water column is 8 cm, top right
to top left.
The initial height difference is h as shown in the figure.
(a) if we set y=0 at the equilibrium height for the water, what is the
value of y, = y (t = 0) for the right column?
(b) When the thumb is removed, what happens during the next several
seconds?
(c) Set up Newton's 2nd law for the water column starting with the pressures.
(d) Compare the result with the oscillator equation and determine the expression for the
angular frequency .
(e) Student I. Maslow Starter began the data collection 0.5[s] after the thumb was
removed. The height y at that time was 0.8yo. Determine the velocity of the water column
at that time in terms of g. p & yo.
(f) Use your values of yo & the initial velocity v, to determine the amplitudes A & B in
y = Acos (at) + B sin(@t) and, from those, find the amplitude D and phase shift d in
y = D cos( ot + 8)
(9) The amplitude of the motion decreases by 10% per period. Determine the damping
constant B in e, the damping coefficient, b in F = -by and the resonance frequency of
the damped oscillator.
Expert Solution
Step 1
(e)
Determine the initial velocity (v0) in the student’s measurement with the given initial displacement (y = 0.8y0) and the value of ω by using the standard formula as follows:
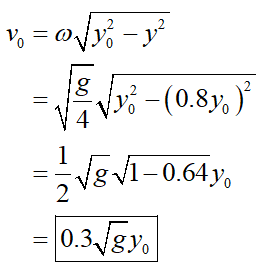
Trending now
This is a popular solution!
Step by step
Solved in 6 steps with 6 images
