(2) A mechanical system is modeled by the system of ODE's. For this system choose X₁ -B-2 x= x₂ = 9 consider the output to be y, and do the following: Determine the state-space matrices A, B, and C Determine the characteristic equation mÿ+k₁y+k₂(y−z)=F c₂ż-k₂(y-z)=0
(2) A mechanical system is modeled by the system of ODE's. For this system choose X₁ -B-2 x= x₂ = 9 consider the output to be y, and do the following: Determine the state-space matrices A, B, and C Determine the characteristic equation mÿ+k₁y+k₂(y−z)=F c₂ż-k₂(y-z)=0
Elements Of Electromagnetics
7th Edition
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Sadiku, Matthew N. O.
ChapterMA: Math Assessment
Section: Chapter Questions
Problem 1.1MA
Related questions
Question
100%
![**Transcription for Educational Use**
**(2) A mechanical system is modeled by the system of ODE's. For this system, choose**
\[
\mathbf{\dot{x}} =
\begin{bmatrix}
x_1 \\
x_2 \\
x_3
\end{bmatrix} =
\begin{bmatrix}
y \\
\dot{y} \\
z
\end{bmatrix}
\]
Consider the output to be \( y \), and do the following:
- Determine the state-space matrices \( A \), \( B \), and \( C \)
- Determine the characteristic equation
\[
m\ddot{y} + k_1 y + k_2 (y - z) = F
\]
\[
c_2 \dot{z} - k_2 (y - z) = 0
\]
**Explanation:**
This text outlines a mechanical system represented by a system of ordinary differential equations (ODEs). In this setup, the state vector \(\mathbf{\dot{x}}\) is defined in terms of variables \(x_1\), \(x_2\), and \(x_3\), which are equated to corresponding variables \(y\), \(\dot{y}\), and \(z\).
The task is to:
1. **Determine the state-space matrices** \( A \), \( B \), and \( C \): These matrices are essential for analyzing and controlling state-space representations of dynamic systems.
2. **Determine the characteristic equation**: This equation is critical in analyzing the stability and dynamics of the system.
The two given equations describe the dynamics of the mechanical system. The first equation relates mass \( m \), damping coefficient \( k_1 \), stiffness \( k_2 \), and an external force \( F \). The second equation describes the relation involving damping \( c_2 \) and stiffness \( k_2 \) with respect to variables \( z \) and \( y \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F811e9e09-f827-40da-a830-8949fa4f6658%2Fd9e1b388-89d7-4606-bcd6-5c717f12e72d%2Fgws3859_processed.png&w=3840&q=75)
Transcribed Image Text:**Transcription for Educational Use**
**(2) A mechanical system is modeled by the system of ODE's. For this system, choose**
\[
\mathbf{\dot{x}} =
\begin{bmatrix}
x_1 \\
x_2 \\
x_3
\end{bmatrix} =
\begin{bmatrix}
y \\
\dot{y} \\
z
\end{bmatrix}
\]
Consider the output to be \( y \), and do the following:
- Determine the state-space matrices \( A \), \( B \), and \( C \)
- Determine the characteristic equation
\[
m\ddot{y} + k_1 y + k_2 (y - z) = F
\]
\[
c_2 \dot{z} - k_2 (y - z) = 0
\]
**Explanation:**
This text outlines a mechanical system represented by a system of ordinary differential equations (ODEs). In this setup, the state vector \(\mathbf{\dot{x}}\) is defined in terms of variables \(x_1\), \(x_2\), and \(x_3\), which are equated to corresponding variables \(y\), \(\dot{y}\), and \(z\).
The task is to:
1. **Determine the state-space matrices** \( A \), \( B \), and \( C \): These matrices are essential for analyzing and controlling state-space representations of dynamic systems.
2. **Determine the characteristic equation**: This equation is critical in analyzing the stability and dynamics of the system.
The two given equations describe the dynamics of the mechanical system. The first equation relates mass \( m \), damping coefficient \( k_1 \), stiffness \( k_2 \), and an external force \( F \). The second equation describes the relation involving damping \( c_2 \) and stiffness \( k_2 \) with respect to variables \( z \) and \( y \).
Expert Solution
Step 1
Given,
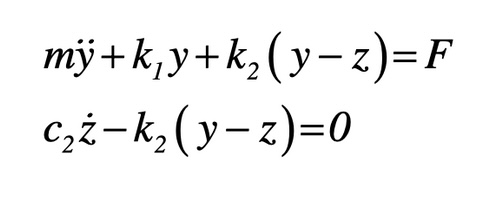
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education

Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education

Control Systems Engineering
Mechanical Engineering
ISBN:
9781118170519
Author:
Norman S. Nise
Publisher:
WILEY

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning

Engineering Mechanics: Statics
Mechanical Engineering
ISBN:
9781118807330
Author:
James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:
WILEY