You wish to determine if there is a linear correlation between the two variables at a significance level ofa = 0.005. You have the following bivariate data set.28.969.760.256.156.884.838.827.748.998.978.361.554.571.750.175.234.493.213.164.2What is the correlation coefficient for this data set?To find the p-value for a correlation coefficient, you need to convert to a t-score:2(n – 2)t =This t-score is from a t-distribution with n-2 degrees of freedom.What is the p-value for this correlation coefficient?p-value =Your final conclusion is that...O There is sufficient sample evidence to support the claim that there is a statistically significantcorrelation between the two variables.O There is insufficient sample evidence to support the claim the there is a correlation between the twovariables.Note: In your calculations, round both r and t to 3 decimal places in ALL calculations.

Name: You wish to determine if there is a linear correlation between the tw
Uploaded: 2024-03-20T07:06:16.000Z
Channel: Bartleby
Description: You wish to determine if there is a linear correlation between the two variables at a significance level ofa = 0.005. You have the following bivariate data set.28.969.760.256.156.884.838.827.748.998.978.361.554.571.750.175.234.493.213.164.2What is t

Answered: 13.1 64.2 What is the correlation…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Concept explainers

Topic Video

Question

You wish to determine if there is a linear correlation between the two variables at a significance level of
a = 0.005. You have the following bivariate data set.
28.9
69.7
60.2
56.1
56.8
84.8
38.8
27.7
48.9
98.9
78.3
61.5
54.5
71.7
50.1
75.2
34.4
93.2
13.1
64.2
What is the correlation coefficient for this data set?
To find the p-value for a correlation coefficient, you need to convert to a t-score:
2(n – 2)
t =
This t-score is from a t-distribution with n-2 degrees of freedom.
What is the p-value for this correlation coefficient?
p-value =
Your final conclusion is that...
O There is sufficient sample evidence to support the claim that there is a statistically significant
correlation between the two variables.
O There is insufficient sample evidence to support the claim the there is a correlation between the two
variables.
Note: In your calculations, round both r and t to 3 decimal places in ALL calculations.

Expert Solution

Step 1

The data for two variables x and y is given in the following table,

x	y
28.9	69.7
60.2	56.1
56.8	84.8
38.8	98.9
27.7	78.3
48.9	61.5
54.5	71.7
50.1	75.2
34.4	93.2
13.1	64.2

It is required to test the significance of correlation.

The given level of significance is 0.005.

Step 2

First calculating the correlation coefficient

It can be calculated using MS-Excel.

Steps for calculating using MS-Excel are as follows

Enter the data in MS-Excel
Click on the Data toolbar >> Select the Data Analysis >>Correlation.
Select the entire data as an input range. (Check labels if included)

The output will be

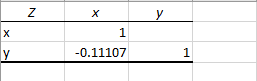
From the above output the correlation coefficient (r) = -0.11107

Rounding to three decimal

r = -0.111

Step 3: Hypothesis

The null and alternative hypothesis is

H0 : $ρ$ = 0

H1 : $ρ$ $\neq 0$

Where $ρ$ is the population correlation coefficient.

The formula for test statistic is

$t = \sqrt{\frac{r^{2} (n - 2)}{1 - r^{2}}}$

$t = \sqrt{\frac{- 0 . 111^{2} (10 - 1)}{1 - 0 . 111^{2}}}$

= 0.3309673

Rounding to three decimal

t =0.331

The degree of freedom for the test is df = n -2 = 8

Step by step

Solved in 5 steps with 1 images

Knowledge Booster

$Centre, Spread, and Shape of a Distribution$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Similar questions