(13) Let X be a random variable that takes only positive values. If E|X| < ∞, prove that E(X) · E(1/X) > 1. (a) Since f (t) = 1/t is a convex function for t > 0, Jensen's inequality gives that E(1/X) > 1/E(X). (b) Since f(t) = 1 = tlt is a convex function for t > 0, Jensen's inequality gives that E(1/X) > 1/E(X). (c) The statement of the problem is, in fact, false. (d) Follows by Markov's inequality (e) Follows by Chebyshev's inequality. The correct answer is (a) (b) (c) (d) (e) N/A (Select One)
(13) Let X be a random variable that takes only positive values. If E|X| < ∞, prove that E(X) · E(1/X) > 1. (a) Since f (t) = 1/t is a convex function for t > 0, Jensen's inequality gives that E(1/X) > 1/E(X). (b) Since f(t) = 1 = tlt is a convex function for t > 0, Jensen's inequality gives that E(1/X) > 1/E(X). (c) The statement of the problem is, in fact, false. (d) Follows by Markov's inequality (e) Follows by Chebyshev's inequality. The correct answer is (a) (b) (c) (d) (e) N/A (Select One)
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question

Transcribed Image Text:(13) Let X be a random variable that takes only positive values. If E|X| < ∞, prove that E(X) · E(1/X) > 1.
(a) Since f (t) = 1/t is a convex function for t > 0, Jensen's inequality gives that E(1/X) > 1/E(X).
(b) Since f(t) = 1 = t/t is a convex function for t > 0, Jensen's inequality gives that E(1/X) > 1/E(X).
(c) The statement of the problem is, in fact, false.
(d) Follows by Markov's inequality.
(e) Follows by Chebyshev's inequality.
The correct answer is
(a)
(b)
(c)
(d)
(е)
N/A
(Select One)
Expert Solution
Step 1
Jensen’s Inequality:
For a continuous and convex function, the Jensen’s inequality is given by
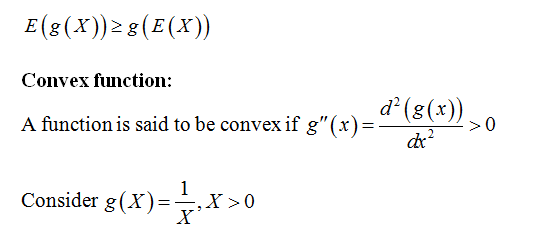
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
