Answered: 10.16. The potential energy in a… | bartleby

Related questions

Question

10.16. The potential energy in a particular anisotropic harmonic oscillator with
cylindrical symmetry is given by
1
V:
with wi < wz < 2w1.
(a) Determine the energy eigenvalues and the degeneracies of the three lowest
energy levels by using Cartesian coordinates.
(b) Solve the energy eigenvalue equation in cylindrical coordinates and check
your results in comparison with those of (a).

Expert Solution

Step 1

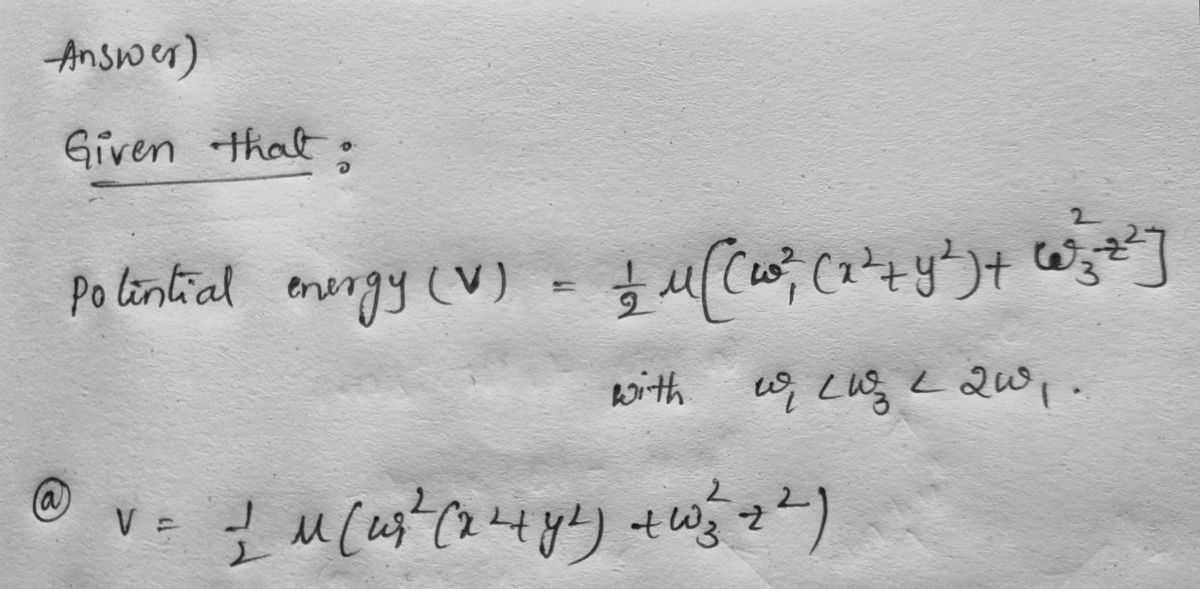
Trending now

This is a popular solution!

Step by step

Solved in 2 steps with 2 images

SEE SOLUTION Check out a sample Q&A here

Blurred answer

Similar questions

An electron is in a finite square well that is 0.6 eV deep, and 2.1 nm wide. Calculate the value of the dimensionless potential (to 3 s.f).
4.1. Using the nearly free-electron approximation for a one-dimensional (1-D) crystal lattice and assuming that the only nonvanishing Fourier coefficients of the crystal potential are v(n/a) and v(-π/a) in (4.73), show that near the band edge at k = 0, the dependence of electron energy on the wave vector k is given by where m* = Ek electron at k = 0. = Eo + = mo[1 − (32m²aª / hªлª)v(π/a)²]¯¹ is the effective mass of the ħ²k² 2m*
Your answer is partially correct. An electron, trapped in a one-dimensional infinite potential well 366 pm wide, is in its ground state. How much energy must it absorb if it is to jump up to the state with n=7? Number 139.6 Units eV
Consider a weakly anharmonic a 1D oscillator with the poten- tial energy m U(x) = w?a² + Ba* 2 Calculate the energy levels in the first order in the small anharmonicity parameter 3 using TIPT and the ladder operators.
Legrende polynomials The amplitude of a stray wave is defined by: SO) =x (21+ 1) exp li8,] sen 8, P(cos 8). INO Here e is the scattering angle, / is the angular momentum and 6, is the phase shift produced by the central potential that performs the scattering. The total cross section is: Show that: 'É4+ 1)sen² 8, .