1. Give an example of a function f N N which is injective but not surjective.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:**Exercise 1: Functions**
**Task:** Give an example of a function \( f : \mathbb{N} \to \mathbb{N} \) which is injective but not surjective.
### Explanation
- **Injective Function (One-to-One):** A function \( f \) is injective if different elements in the domain map to different elements in the codomain. Formally, \( f(a) = f(b) \) implies \( a = b \).
- **Surjective Function (Onto):** A function \( f \) is surjective if every element in the codomain has a pre-image in the domain. There are no elements in the codomain left unmapped.
**Example Solution:**
Consider the function \( f(n) = n + 1 \).
- **Injectivity:** If \( f(a) = f(b) \), then \( a + 1 = b + 1 \), which implies \( a = b \). Therefore, \( f \) is injective.
- **Not Surjective:** The element 0 in the codomain \(\mathbb{N}\) (if we include 0 in natural numbers) does not have a pre-image, as no natural number \( n \) satisfies \( n + 1 = 0 \). Thus, \( f \) is not surjective.
Expert Solution
Step 1
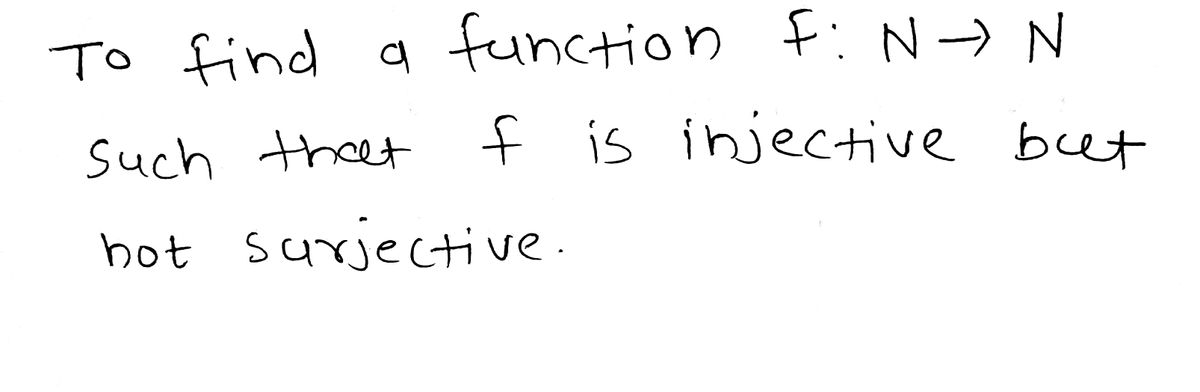
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

