1. For a and b, conduct every step of the Hypothesis testing process (1-5).The distribution of SAT scores is normal with M = 500, with a standard deviation alpha = 100. Mable believes that she scored significantly higher than average, at x = 643. Did Mable scores significantly higher than the average SAT score?A sample of n = 30 adults is taken from the above population and their average SAT score is measured to be M = 507. Does this sample differ from the population?

Name: 1. For a and b, conduct every step of the Hypothesis testing process (
Uploaded: 2024-03-20T07:07:12.000Z
Channel: Bartleby
Description: 1. For a and b, conduct every step of the Hypothesis testing process (1-5).The distribution of SAT scores is normal with M = 500, with a standard deviation alpha = 100. Mable believes that she scored significantly higher than average, at x = 643. Did

Answered: 1. For a and b, conduct every step of…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Topic Video

Question

1. For a and b, conduct every step of the Hypothesis testing process (1-5).

The distribution of SAT scores is normal with M = 500, with a standard deviation alpha = 100. Mable believes that she scored significantly higher than average, at x = 643. Did Mable scores significantly higher than the average SAT score?
A sample of n = 30 adults is taken from the above population and their average SAT score is measured to be M = 507. Does this sample differ from the population?

Expert Solution

Step 1

1. The null and alternative hypothesis is given by;

$H_{0} : μ = 500 H_{a} : μ > 500 L e t t h e l e v e l o f s i g n i f i c a n c e b e α = 0.05 G i v e n; x = 643 n = 1 σ = 100 T h e t e s t s t a t i s t i c i s g i v e n b y; z = \frac{\sqrt{n} (x - μ)}{σ} = \frac{\sqrt{1} (643 - 500)}{100} = 1.43 T h e c r i t i c a l v a l u e i s g i v e n b y; z_{α} = z_{0.05} W e u s e E x c e l t o f i n d t h e c r i t i c a l v a l u e;$

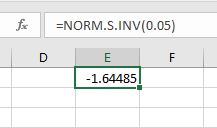
Hence the critical value is;

z_0.05 = 1.645 [Since Normal Distribution is symmetric]

Here;

z < z_0.05

We accept the null hypothesis. Hence Mable did not score significantly higher than the average SAT score.

Trending now

This is a popular solution!

Step by step

Solved in 2 steps with 2 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Hypothesis Tests and Confidence Intervals for Means$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Similar questions