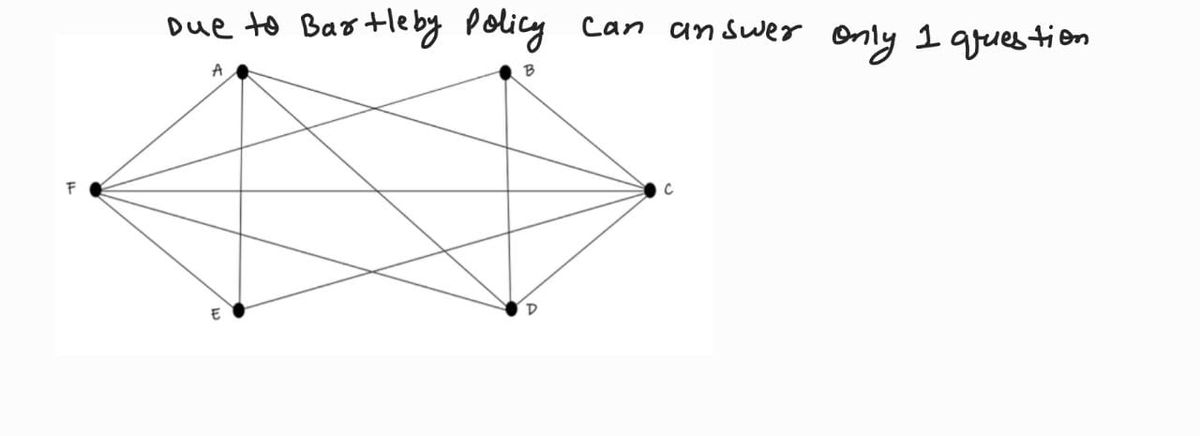
1) Consider the following graph: 71 A E B a) Does it have a Hamilton Circuit? If so, give the circuit. If not, briefly explain why not. с
1) Consider the following graph: 71 A E B a) Does it have a Hamilton Circuit? If so, give the circuit. If not, briefly explain why not. с
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:Certainly! Here is a transcription and explanation suitable for an educational website:
---
### Graph Theory Problem
#### 1) Consider the following graph:
**Description:**
The graph consists of 6 vertices labeled A, B, C, D, E, and F, forming a bipartite structure. Each vertex on the left (F, E) is connected to all vertices on the right (A, B, C, D), and vice versa.
**Questions:**
a) **Hamiltonian Circuit:**
- **Task:** Determine if a Hamiltonian Circuit exists in the graph. If it does, provide the circuit. If it does not, briefly explain why not.
b) **Euler Circuit:**
- **Observation:** The graph does not possess an Euler Circuit. Explain why this is the case.
- **Question:** What is the minimum number of edges required to be retraced (duplicated) to Eulerize the graph? List these edges if possible.
- **Additional Task:** Provide the circuit that solves the Chinese Postman problem for this graph.
**Notes:**
- A **Hamiltonian Circuit** visits every vertex exactly once and returns to the starting vertex.
- An **Euler Circuit** uses every edge exactly once and returns to the starting vertex.
- The **Chinese Postman Problem** seeks a circuit that minimizes the total distance traveled by covering each edge at least once.
---
This transcription and explanation help present the conceptual and practical aspects of graph theory in the context of Hamiltonian and Euler circuits and introduce the Chinese Postman problem.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

