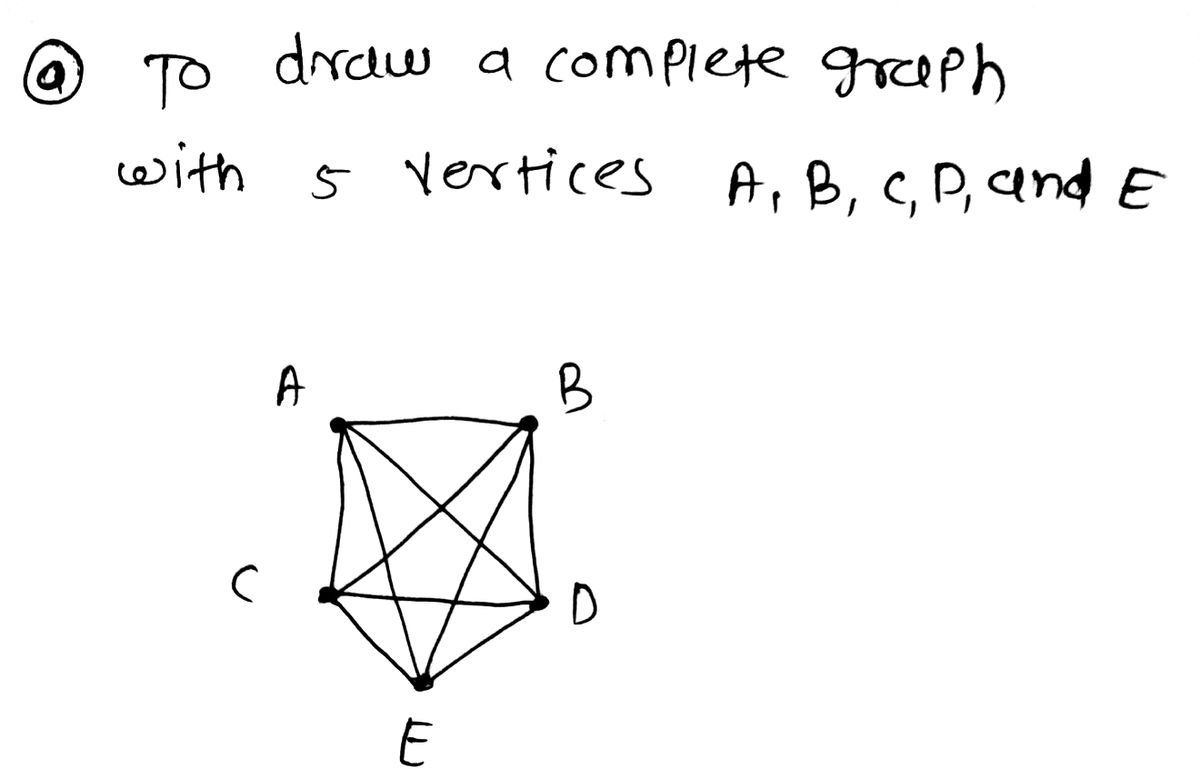
Question 3 Draw a complete graph with five vertices labeled A, B, C, D, and E. a. b. Find one Hamiltonian circuit for the graph in a. the larg How many edges would a complete graph with n vertices contain? с.
Question 3 Draw a complete graph with five vertices labeled A, B, C, D, and E. a. b. Find one Hamiltonian circuit for the graph in a. the larg How many edges would a complete graph with n vertices contain? с.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
need help with all three questions

Transcribed Image Text:**Question 3**
a. Draw a *complete graph* with five vertices labeled A, B, C, D, and E.
b. Find one *Hamiltonian circuit* for the graph in a.
c. How many edges would a *complete graph* with *n* vertices contain?
**Graph Explanation:**
- The instructions refer to a complete graph, which means every vertex is connected to every other vertex by a unique edge.
- A Hamiltonian circuit involves a path that visits each vertex once and returns to the starting vertex.
- The formula for determining the number of edges in a complete graph with *n* vertices is \( \frac{n(n-1)}{2} \). For example, with five vertices (A, B, C, D, E), the graph would contain \( \frac{5(5-1)}{2} = 10 \) edges.
Expert Solution
Step 1
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

