-1 4 and v = 2 u = 2 (a) Are u and v orthogonal? (b) What is the distance between u and v? (c) Find a unit vector in the direction of u. (;)-
-1 4 and v = 2 u = 2 (a) Are u and v orthogonal? (b) What is the distance between u and v? (c) Find a unit vector in the direction of u. (;)-
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![### Vector Analysis Problem Set
**(1) Let**
\[
\mathbf{u} = \begin{pmatrix} -1 \\ 2 \end{pmatrix} \quad \text{and} \quad \mathbf{v} = \begin{pmatrix} 4 \\ 2 \end{pmatrix}.
\]
**Questions:**
(a) Are **u** and **v** orthogonal?
(b) What is the distance between **u** and **v**?
(c) Find a unit vector in the direction of **u**.
---
### Explanation
In this problem, we are given two vectors in two-dimensional space and are asked to perform several operations:
1. **Orthogonality Check:**
- Two vectors are orthogonal if their dot product is zero. Compute \(\mathbf{u} \cdot \mathbf{v}\).
2. **Distance Calculation:**
- The distance between two vectors is given by the Euclidean distance formula: \(\text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\).
3. **Unit Vector:**
- A unit vector in the direction of \(\mathbf{u}\) is found by dividing each component of \(\mathbf{u}\) by its magnitude: \(\|\mathbf{u}\|\). The magnitude of a vector \(\mathbf{u} = \begin{pmatrix} x \\ y \end{pmatrix}\) is \(\sqrt{x^2 + y^2}\).
Use these principles to solve the given tasks related to vectors \(\mathbf{u}\) and \(\mathbf{v}\).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F87bd9bd0-40fd-4172-a50a-abb52eb6a8c1%2Fd8de2924-e894-466d-8a11-f6e218d47e40%2Fbikdcxh_processed.png&w=3840&q=75)
Transcribed Image Text:### Vector Analysis Problem Set
**(1) Let**
\[
\mathbf{u} = \begin{pmatrix} -1 \\ 2 \end{pmatrix} \quad \text{and} \quad \mathbf{v} = \begin{pmatrix} 4 \\ 2 \end{pmatrix}.
\]
**Questions:**
(a) Are **u** and **v** orthogonal?
(b) What is the distance between **u** and **v**?
(c) Find a unit vector in the direction of **u**.
---
### Explanation
In this problem, we are given two vectors in two-dimensional space and are asked to perform several operations:
1. **Orthogonality Check:**
- Two vectors are orthogonal if their dot product is zero. Compute \(\mathbf{u} \cdot \mathbf{v}\).
2. **Distance Calculation:**
- The distance between two vectors is given by the Euclidean distance formula: \(\text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\).
3. **Unit Vector:**
- A unit vector in the direction of \(\mathbf{u}\) is found by dividing each component of \(\mathbf{u}\) by its magnitude: \(\|\mathbf{u}\|\). The magnitude of a vector \(\mathbf{u} = \begin{pmatrix} x \\ y \end{pmatrix}\) is \(\sqrt{x^2 + y^2}\).
Use these principles to solve the given tasks related to vectors \(\mathbf{u}\) and \(\mathbf{v}\).
Expert Solution
Step 1
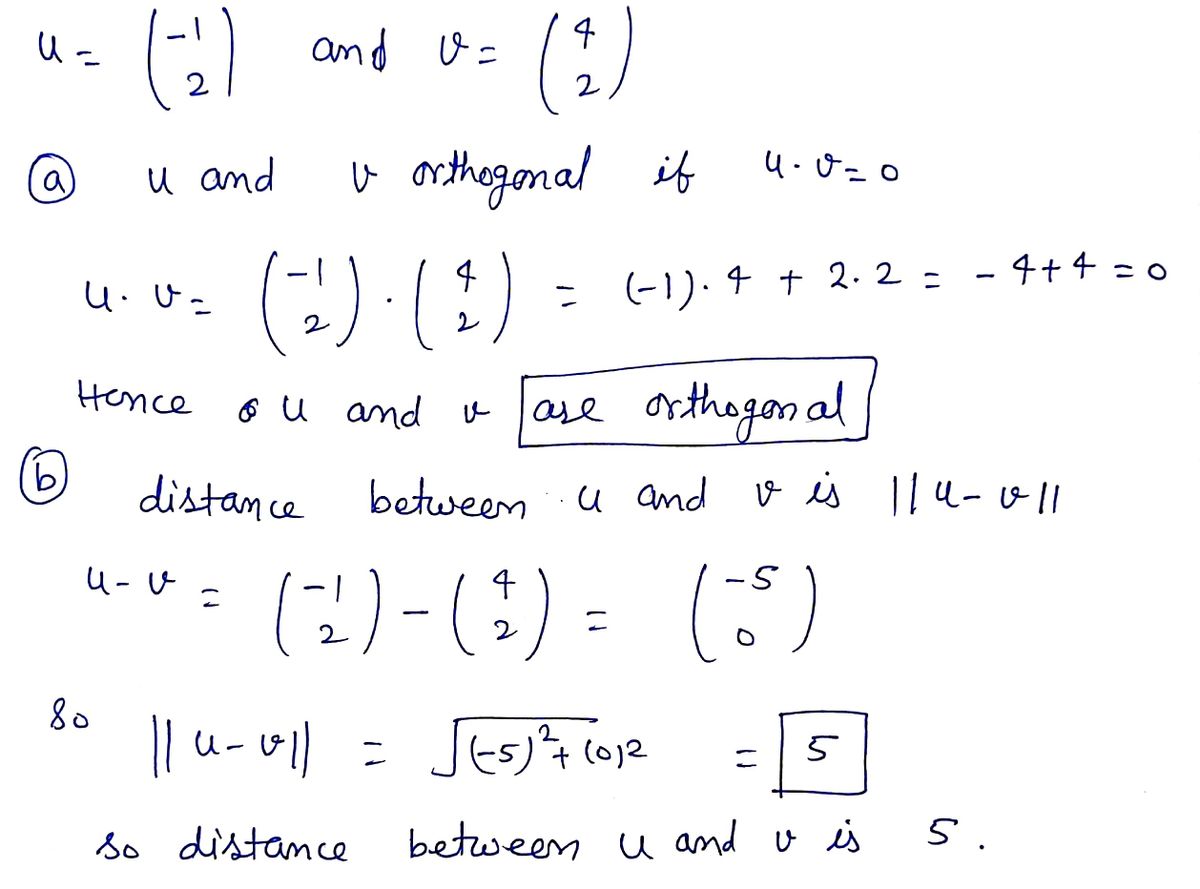
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

