Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
. Maximum profit occurs at those x-values for which R'(x) = C'(x) and R"(x) < C"(x), where R(x) is the total revenue and C(x) is the total cost when x units are produced. 16. Maximizing area. A rancher wants to enclose two rectangular areas near a river, one for sheep and one for cattle. The rancher has 240 yd of fencing available. What is the largest total area that can be enclosed?

. Maximum profit occurs at those x-values for which R'(x) = C'(x) and R"(x) < C"(x), where R(x) is the total revenue and C(x) is the total cost when x units are produced. 16. Maximizing area. A rancher wants to enclose two rectangular areas near a river, one for sheep and one for cattle. The rancher has 240 yd of fencing available. What is the largest total area that can be enclosed?

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
100%
In the problem I am trying to maximize the area for number 16. My constraint is 240 yd of fence. I added a picture of my work to see if I was on the right track. I assume that I could multiple the x•y twice. The additional x is throwing me off
s.pearson.com OneLogin Applications of Differentiation mine tion has tive 70. has tive 50. air he 1 ir that jective 4. mbers Week 8 W... mbers E Section 3.5 P Page 328 . Maximum profit occurs at those x-values for which R'(x) = C'(x) and R"(x) < C"(x), where R(x) is the total revenue and C(x) is the total cost when x units are produced. 16. Maximizing area. A rancher wants to enclose two rectangular areas near a river, one for sheep and one for cattle. The rancher has 240 yd of fencing available. What is the largest total area that can be enclosed? 17. Maximizing area. Grayson Farms plans to enclose three parallel rectangular livestock pens within one large rectangular area using 600 m of fencing. One side of the a is a pre-existing stone wall. M Coffee M
Transcribed Image Text:s.pearson.com OneLogin Applications of Differentiation mine tion has tive 70. has tive 50. air he 1 ir that jective 4. mbers Week 8 W... mbers E Section 3.5 P Page 328 . Maximum profit occurs at those x-values for which R'(x) = C'(x) and R"(x) < C"(x), where R(x) is the total revenue and C(x) is the total cost when x units are produced. 16. Maximizing area. A rancher wants to enclose two rectangular areas near a river, one for sheep and one for cattle. The rancher has 240 yd of fencing available. What is the largest total area that can be enclosed? 17. Maximizing area. Grayson Farms plans to enclose three parallel rectangular livestock pens within one large rectangular area using 600 m of fencing. One side of the a is a pre-existing stone wall. M Coffee M
1 $6a Week 8 Home work Constraint 240 yards of france MI Y 6. (x+y)+x) = aya 3- ухо x 30 (x+y)+x= 120 + X IX-X y=1a0-ax A(x) = x (120-2x) A(x)=120x-2x A'(x) = 120 - 4x = -10 100 150 180 210 Xx=-120 |x = 30 -प y = no-2 (3) = 60 (y=60)
Transcribed Image Text:1 $6a Week 8 Home work Constraint 240 yards of france MI Y 6. (x+y)+x) = aya 3- ухо x 30 (x+y)+x= 120 + X IX-X y=1a0-ax A(x) = x (120-2x) A(x)=120x-2x A'(x) = 120 - 4x = -10 100 150 180 210 Xx=-120 |x = 30 -प y = no-2 (3) = 60 (y=60)
Expert Solution
Step 1

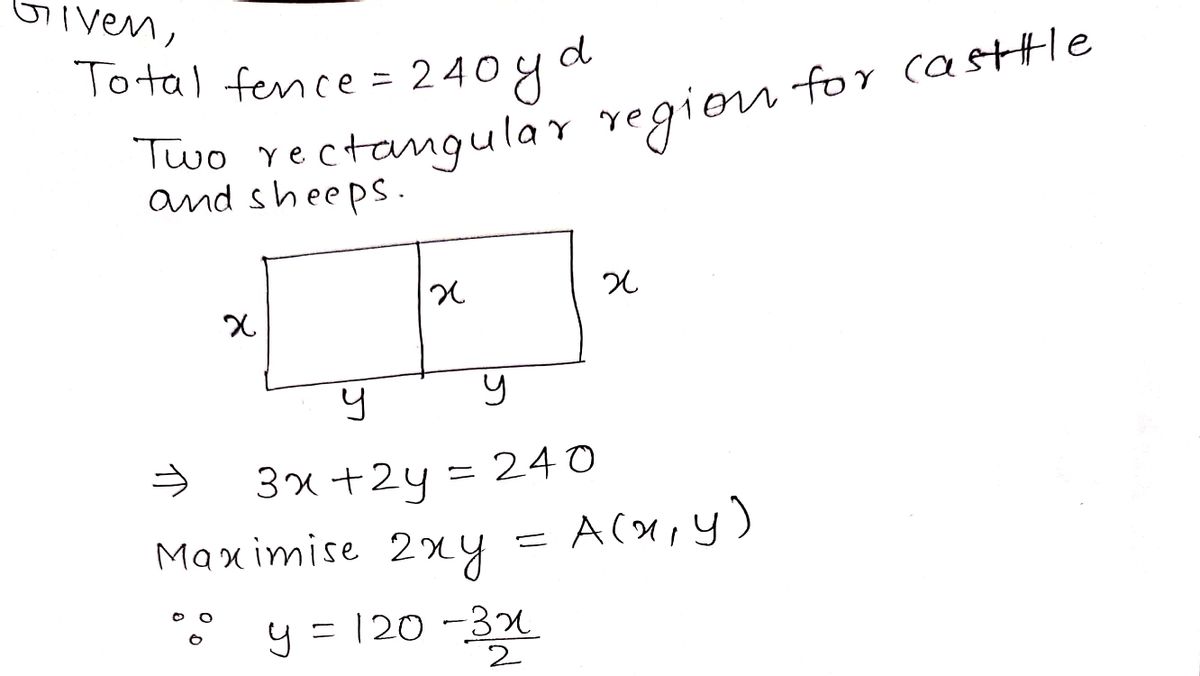
Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS