
Concept explainers
Graph:
To graph: The system of inequalities
Explanation of Solution
Given Information:
The system of inequalities
Graph:
Consider the provided system of inequalities.
To graph the linear inequality
Compute some points on the graph of linear equation
Substitute
So,
Substitute
So,
Substitute
So,
Plot all three points
The graph of the linear equation
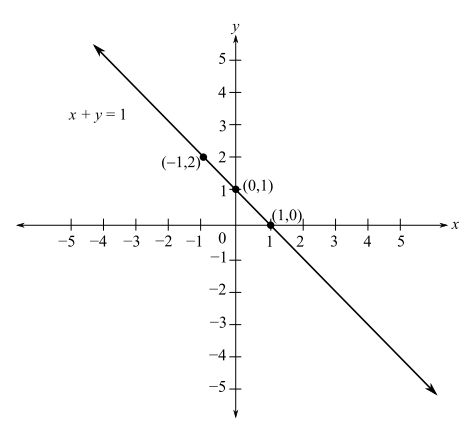
Take
This is false.
So, the region on the opposite side of point
Shade all points on that side of the line using pink shading.

To graph the linear inequality
Compute some points on the graph of linear equation
Substitute
So,
Substitute
So,
Substitute
So,
Plot all three points
The graph of the linear equation
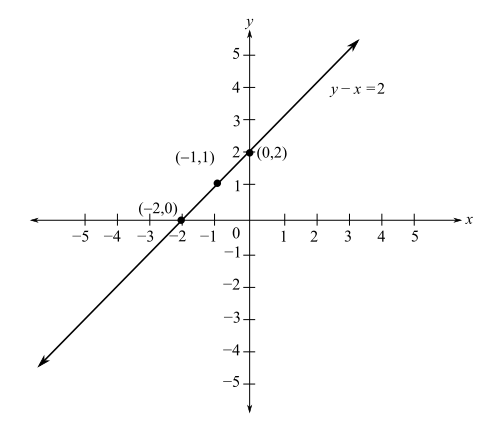
Take
This is false.
So, the region on the opposite side of point
Shade all points on that side of the line using sky blue shading.

Draw both inequalities on the same graph paper. The intersection of two graphs is as follows
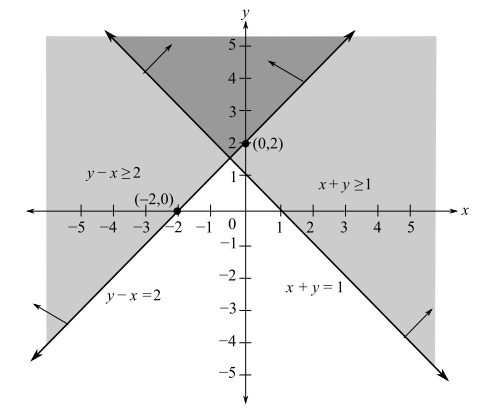
The grey region in the above graph represents the solution of the system of inequalities.
Want to see more full solutions like this?
Chapter M Solutions
DEVELOP.MATH(3 VOLS) CUSTOM-W/MML <IC<
- Class, the class silues, and the class notes, whether the series does alternate and the absolute values of the terms decrease), and if the test does apply, determine whether the series converges or diverges. For the ith series, if the test does not apply the let Mi = 2, while if the test determines divergence then M¿ = 4, and if it determines convergence then M¿ = 8. 1: 2: 3 : 4: 5 : ∞ n=1 ∞ (−1)n+1. Σ(-1) +1 n=1 ∞ п 3m² +2 Σ(-1)+1 sin(2n). n=1 ∞ 2n² + 2n +3 4n2 +6 1 e-n + n² 3n23n+1 9n² +3 In(n + 1) 2n+1 Σ(-1) +1 n=1 ∞ Σ(-1)". n=1 Then the value of cos(M₁) + cos(2M2) + cos(3M3) + sin(2M4) + sin(M5) is 1.715 0.902 0.930 -1.647 -0.057 ● 2.013 1.141 4.274arrow_forward3. FCX14) = x²+3xx-y3 +.arrow_forwardBH is tangent to circle A and DF is a diameter. I don't know where to go from here. May you help please?arrow_forward
- A cylindrical chemical storage tank with a capacity of 950m3 is going to be constructed in a warehouse that is 11m by 14m with a height of 10m. The specifications call for the case to be made of sheet metal that costs $90/m2, the top to be made from sheet metal that costs $45/m2 and the wall to be made of sheet metal that costs $80/m2. If you want to minimize the cost to make the storage house, how much would you end up spending to build the tank?arrow_forwardCalculate the max value of the directional derivatearrow_forwardselect bmw stock. you can assume the price of the stockarrow_forward
- This problem is based on the fundamental option pricing formula for the continuous-time model developed in class, namely the value at time 0 of an option with maturity T and payoff F is given by: We consider the two options below: Fo= -rT = e Eq[F]. 1 A. An option with which you must buy a share of stock at expiration T = 1 for strike price K = So. B. An option with which you must buy a share of stock at expiration T = 1 for strike price K given by T K = T St dt. (Note that both options can have negative payoffs.) We use the continuous-time Black- Scholes model to price these options. Assume that the interest rate on the money market is r. (a) Using the fundamental option pricing formula, find the price of option A. (Hint: use the martingale properties developed in the lectures for the stock price process in order to calculate the expectations.) (b) Using the fundamental option pricing formula, find the price of option B. (c) Assuming the interest rate is very small (r ~0), use Taylor…arrow_forwardQuestion 1. Prove that the function f(x) = 2; f: (2,3] → R, is not uniformly continuous on (2,3].arrow_forwardCalculus III May I please have the example, definition semicolons, and all blanks completed and solved? Thank you so much,arrow_forward

 Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University





