Path To College Mathematics
1st Edition
ISBN: 9780134654409
Author: Martin-Gay, K. Elayn, 1955-
Publisher: Pearson,
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter E, Problem 35ES
The distance a spring stretches varies directly with the weight attached to the spring. If a
-pound weight stretches the spring
-pound weight stretches the spring.
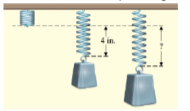
If a
-pound weight stretches a spring
-pound weight stretches the spring (See Exercise 35.)
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Q4: Discuss the stability critical point of the ODES x + sin(x) = 0 and draw
phase portrait.
Using Karnaugh maps and Gray coding, reduce the following circuit represented as a table and write the final circuit in simplest form (first in terms of number of gates then in terms of fan-in of those gates). HINT: Pay closeattention to both the 1’s and the 0’s of the function.
Recall the RSA encryption/decryption system. The following questions are based on RSA. Suppose n (=15) is the product of the two prime numbers 3 and 5.1. Find an encryption key e for for the pair (e, n)2. Find a decryption key d for for the pair (d, n)3. Given the plaintext message x = 3, find the ciphertext y = x^(e) (where x^e is the message x encoded with encryption key e)4. Given the ciphertext message y (which you found in previous part), Show that the original message x = 3 can be recovered using (d, n)
Chapter E Solutions
Path To College Mathematics
Ch. E - Write a direct variation equation, y=kx, that...Ch. E - Write a direct variation equation, y=kx, that...Ch. E - Write a direct variation equation, y=kx, that...Ch. E - Write a direct variation equation, y=kx, that...Ch. E - Write a direct variation equation, y=kx, that...Ch. E - Write a direct variation equation, y=kx, that...Ch. E - Write a direct variation equation, y=kx, that...Ch. E - Write a direct variation equation, y=kx, that...Ch. E - Write an inverse variation equation, y=kx, that...Ch. E - Write an inverse variation equation, y=kx, that...
Ch. E - Write an inverse variation equation, y=kx, that...Ch. E - Write an inverse variation equation, y=kx, that...Ch. E - Write en equation to describe each variation Use k...Ch. E - Write en equation to describe each variation Use k...Ch. E - Write en equation to describe each variation Use k...Ch. E - Write en equation to describe each variation Use k...Ch. E - Write en equation to describe each variation Use k...Ch. E - Write en equation to describe each variation Use k...Ch. E - Write en equation to describe each variation Use k...Ch. E - Write en equation to describe each variation Use k...Ch. E - Write en equation to describe each variation Use k...Ch. E - Write en equation to describe each variation Use...Ch. E - Solve. See Examples 2, 5, and 6. y varies directly...Ch. E - Solve. See Examples 2, 5, and 6. y varies directly...Ch. E - Solve. See Examples 2, 5, and 6. y varies directly...Ch. E - Solve. See Examples 2, 5, and 6. y varies directly...Ch. E - Solve. See Examples 2, 5, and 6. z varies directly...Ch. E - Solve. See Examples 2, 5, and 6. s varies directly...Ch. E - Solve. See Examples 2, 5, and 6. a varies...Ch. E - Solve. See Examples 2, 5, and 6. p varies...Ch. E - Solve. If needed, round money amounts to 2 decimal...Ch. E - Solve. If needed, round money amounts to 2 decimal...Ch. E - Solve. If needed, round money amounts to 2 decimal...Ch. E - Solve. If needed, round money amounts to 2 decimal...Ch. E - The distance a spring stretches varies directly...Ch. E - The weight of an object varies inversely as the...Ch. E - For a constant distance, the rate of travel varies...Ch. E - The distanced that an object fails is directly...Ch. E - The distance needed for a car to stop d, is...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Theorem 1: A number n ∈ N is divisible by 3 if and only if when n is writtenin base 10 the sum of its digits is divisible by 3. As an example, 132 is divisible by 3 and 1 + 3 + 2 is divisible by 3.1. Prove Theorem 1 2. Using Theorem 1 construct an NFA over the alphabet Σ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}which recognizes the language {w ∈ Σ^(∗)| w = 3k, k ∈ N}.arrow_forwardRecall the RSA encryption/decryption system. The following questions are based on RSA. Suppose n (=15) is the product of the two prime numbers 3 and 5.1. Find an encryption key e for for the pair (e, n)2. Find a decryption key d for for the pair (d, n)3. Given the plaintext message x = 3, find the ciphertext y = x^(e) (where x^e is the message x encoded with encryption key e)4. Given the ciphertext message y (which you found in previous part), Show that the original message x = 3 can be recovered using (d, n)arrow_forwardFind the sum of products expansion of the function F(x, y, z) = ¯x · y + x · z in two ways: (i) using a table; and (ii) using Boolean identities.arrow_forward
- Give both a machine-level description (i.e., step-by-step description in words) and a state-diagram for a Turing machine that accepts all words over the alphabet {a, b} where the number of a’s is greater than or equal to the number of b’s.arrow_forwardCompute (7^ (25)) mod 11 via the algorithm for modular exponentiation.arrow_forwardProve that the sum of the degrees in the interior angles of any convex polygon with n ≥ 3 sides is (n − 2) · 180. For the base case, you must prove that a triangle has angles summing to 180 degrees. You are permitted to use thefact when two parallel lines are cut by a transversal that corresponding angles are equal.arrow_forward
- Answer the following questions about rational and irrational numbers.1. Prove or disprove: If a and b are rational numbers then a^b is rational.2. Prove or disprove: If a and b are irrational numbers then a^b is irrational.arrow_forwardProve the following using structural induction: For any rooted binary tree T the number of vertices |T| in T satisfies the inequality |T| ≤ (2^ (height(T)+1)) − 1.arrow_forward(a) Prove that if p is a prime number and p|k^2 for some integer k then p|k.(b) Using Part (a), prove or disprove: √3 ∈ Q.arrow_forward
- Provide a context-free grammar for the language {a^ (i) b^ (j) c^ (k) | i, j, k ∈ N, i = j or i = k}. Briefly explain (no formal proof needed) why your context-free grammar is correct and show that it produces the word aaabbccc.arrow_forwardThe Martinezes are planning to refinance their home. The outstanding balance on their original loan is $150,000. Their finance company has offered them two options. (Assume there are no additional finance charges. Round your answers to the nearest cent.) Option A: A fixed-rate mortgage at an interest rate of 4.5%/year compounded monthly, payable over a 30-year period in 360 equal monthly installments.Option B: A fixed-rate mortgage at an interest rate of 4.25%/year compounded monthly, payable over a 12-year period in 144 equal monthly installments. (a) Find the monthly payment required to amortize each of these loans over the life of the loan. option A $ option B $ (b) How much interest would the Martinezes save if they chose the 12-year mortgage instead of the 30-year mortgage?arrow_forwardThe Martinezes are planning to refinance their home. The outstanding balance on their original loan is $150,000. Their finance company has offered them two options. (Assume there are no additional finance charges. Round your answers to the nearest cent.) Option A: A fixed-rate mortgage at an interest rate of 4.5%/year compounded monthly, payable over a 30-year period in 360 equal monthly installments.Option B: A fixed-rate mortgage at an interest rate of 4.25%/year compounded monthly, payable over a 12-year period in 144 equal monthly installments. (a) Find the monthly payment required to amortize each of these loans over the life of the loan. option A $ option B $ (b) How much interest would the Martinezes save if they chose the 12-year mortgage instead of the 30-year mortgage?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Use of ALGEBRA in REAL LIFE; Author: Fast and Easy Maths !;https://www.youtube.com/watch?v=9_PbWFpvkDc;License: Standard YouTube License, CC-BY
Compound Interest Formula Explained, Investment, Monthly & Continuously, Word Problems, Algebra; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=P182Abv3fOk;License: Standard YouTube License, CC-BY
Applications of Algebra (Digit, Age, Work, Clock, Mixture and Rate Problems); Author: EngineerProf PH;https://www.youtube.com/watch?v=Y8aJ_wYCS2g;License: Standard YouTube License, CC-BY