Prealgebra & Introductory Algebra (5th Edition) (What's New in Developmental Math)
5th Edition
ISBN: 9780134707631
Author: Elayn Martin-Gay
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
Chapter D, Problem 1E
To determine
To graph:
The solutions for the provided system of linear inequalities.
Expert Solution & Answer
Answer to Problem 1E
Solution:
The solutions of the system is the region contained in the graphs of both inequalities.
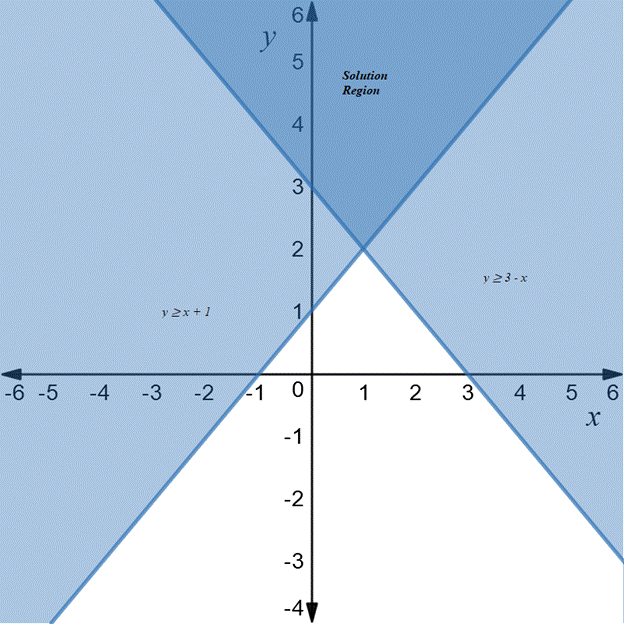
Explanation of Solution
Given:
The provided system of linear inequalities is
Procedure:
Graphing the solutions of a system of linear inequalities:
Step 1: Graph each inequality in the system on the same set of axes.
Step 2: The solutions of the system are the points common to the graphs of all the inequalities in the system.
Calculation:
Consider the inequalities
Graph both the inequalities on the same set of axes.
Since both the inequality symbols are
The solutions of the system are the regions shown by the darkest shading in the graph below.
Graph:
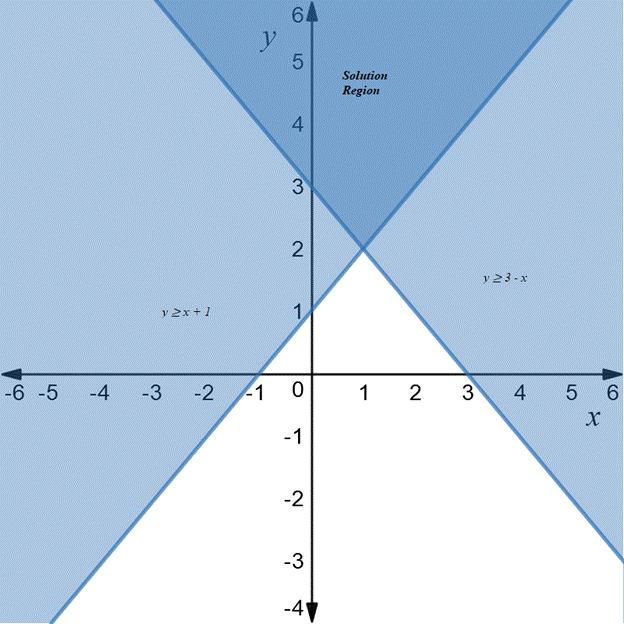
Therefore, the solutions of the system is the region contained in the graphs of both inequalities.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Consider the ceocomp dataset of compensation information for the CEO’s of 100 U.S. companies. We wish to fit aregression model to assess the relationship between CEO compensation in thousands of dollars (includes salary andbonus, but not stock gains) and the following variates:AGE: The CEOs age, in yearsEDUCATN: The CEO’s education level (1 = no college degree; 2 = college/undergrad. degree; 3 = grad. degree)BACKGRD: Background type(1= banking/financial; 2 = sales/marketing; 3 = technical; 4 = legal; 5 = other)TENURE: Number of years employed by the firmEXPER: Number of years as the firm CEOSALES: Sales revenues, in millions of dollarsVAL: Market value of the CEO's stock, in natural logarithm unitsPCNTOWN: Percentage of firm's market value owned by the CEOPROF: Profits of the firm, before taxes, in millions of dollars1) Create a scatterplot matrix for this dataset. Briefly comment on the observed relationships between compensationand the other variates.Note that companies with negative…
6 (Model Selection, Estimation and Prediction of GARCH) Consider the daily returns rt
of General Electric Company stock (ticker: "GE") from "2021-01-01" to "2024-03-31",
comprising a total of 813 daily returns. Using the "fGarch" package of R, outputs of
fitting three GARCH models to the returns are given at the end of this question.
Model 1 ARCH (1) with standard normal innovations;
Model 2
Model 3
GARCH (1, 1) with Student-t innovations;
GARCH (2, 2) with Student-t innovations;
Based on the outputs, answer the following questions.
(a) What can be inferred from the Standardized Residual Tests conducted on Model 1?
(b) Which model do you recommend for prediction between Model 2 and Model 3?
Why?
(c) Write down the fitted model for the model that you recommended in Part (b).
(d) Using the model recommended in Part (b), predict the conditional volatility in the
next trading day, specifically trading day 814.
4 (MLE of ARCH) Suppose rt follows ARCH(2) with E(rt) = 0,
rt = ut, ut =
στει, σε
where {+} is a sequence of independent and identically distributed (iid) standard normal
random variables.
With observations r₁,...,, write down the log-likelihood function for the model esti-
mation.
Chapter D Solutions
Prealgebra & Introductory Algebra (5th Edition) (What's New in Developmental Math)
Ch. D - Prob. 1ECh. D - Prob. 2ECh. D - Prob. 3ECh. D - Prob. 4ECh. D - Prob. 5ECh. D - Prob. 6ECh. D - Prob. 7ECh. D - Prob. 8ECh. D - Prob. 9ECh. D - Prob. 10E
Ch. D - Prob. 11ECh. D - Prob. 12ECh. D - Prob. 13ECh. D - Prob. 14ECh. D - Prob. 15ECh. D - Prob. 16ECh. D - Prob. 17ECh. D - Prob. 18ECh. D - Prob. 19ECh. D - Prob. 20ECh. D - Prob. 21ECh. D - Prob. 22ECh. D - Prob. 23ECh. D - Prob. 24ECh. D - Prob. 25ECh. D - Prob. 26ECh. D - Prob. 27ECh. D - Prob. 28E
Knowledge Booster
Similar questions
- 5 (Moments of GARCH) For the GARCH(2,2) model rt = 0.2+0.25u1+0.05u-2 +0.30% / -1 +0.20% -2, find cov(rt). 0.0035 ut, ut = στει,στ =arrow_forward(14 points) Let S = {(x, y, z) | z = e−(x²+y²), x² + y² ≤ 1}. The surface is the graph of ze(+2) sitting over the unit disk.arrow_forwardDoor 87.5in to 47 living 44.75 Closet 96in Window ISS.Sin 48in Train Table 96in 48in 132:2 Windowarrow_forward
- Classify the singularities for the following functions at the given point. at a = (a) f(z) = 1 (2 sin z-1)² (b) f(z) = exp(4)-1 at 0 and at a = (c) f(z) = 1-cosh z at a=0 2 In the case of a pole, indicate the order of the pole and its residue.arrow_forwardDefinition of null hypothesis from the textbook Definition of alternative hypothesis from the textbook Imagine this: you suspect your beloved Chicken McNugget is shrinking. Inflation is hitting everything else, so why not the humble nugget too, right? But your sibling thinks you’re just being dramatic—maybe you’re just extra hungry today. Determined to prove them wrong, you take matters (and nuggets) into your own hands. You march into McDonald’s, get two 20-piece boxes, and head home like a scientist on a mission. Now, before you start weighing each nugget like they’re precious gold nuggets, let’s talk hypotheses. The average weight of nuggets as mentioned on the box is 16 g each. Develop your null and alternative hypotheses separately. Next, you weigh each nugget with the precision of a jeweler and find they average out to 15.5 grams. You also conduct a statistical analysis, and the p-value turns out to be 0.01. Based on this information, answer the following questions. (Remember,…arrow_forwardBusiness Discussarrow_forward
- Determine all functions f analytic in the open unit disc || < 1 which satisfy in addition f(0) = 1 and |f(z)|≥ 1 whenever || < 1. Justify your answer.arrow_forwardDeduce the Laurent expansion for f(z) = 22(2-3)2 in the annulus 0 < |z3|< 3.arrow_forwardWhat can you conclude about a complex-valued function f(z) that satisfies 1. f is complex differentiable everywhere 2. ƒ(z+1) = ƒ(z) for all z 3. For a fixed complex number a with nonzero imaginary part, f(z+a) = f(z) for all z ? Justify your answer. (Hint: Use Liouville's theorem.)arrow_forward
- 6. Solve the system of differential equations using Laplace Transforms: x(t) = 3x₁ (t) + 4x2(t) x(t) = -4x₁(t) + 3x2(t) x₁(0) = 1,x2(0) = 0arrow_forward3. Determine the Laplace Transform for the following functions. Show all of your work: 1-t, 0 ≤t<3 a. e(t) = t2, 3≤t<5 4, t≥ 5 b. f(t) = f(tt)e-3(-) cos 4τ drarrow_forward4. Find the inverse Laplace Transform Show all of your work: a. F(s) = = 2s-3 (s²-10s+61)(5-3) se-2s b. G(s) = (s+2)²arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education