Chapter CR, Problem 4E

a.

To determine

Explain the relationship between speed and density.

Explanation of Solution

Given info:

The data related to the speed and density of traffic at the same location of a city at 10 different times within a span of 3 months.

Calculation:

Scatterplot:

Software procedure:

Step by step procedure to draw scatterplot using MINITAB software is given as,

• Choose Graph > Scatterplot.
• Choose Simple, and then click OK.
• In Y-variables, enter the column of Speed.
• In X-variables enter the column of Density.
• Click OK.

Output using MINITAB software is given as,

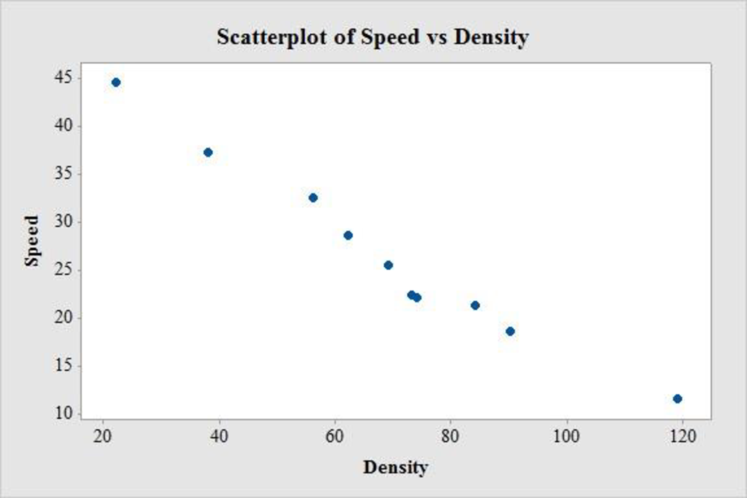
The relation between speed and density is strong, negative and linear. Thus, the association between speed and density is associated with lower speeds.

b.

To determine

Obtain a linear model to predict speed from density and comment on the appropriateness of the model.

Answer to Problem 4E

The regression equation of linear model is $\widehat{\text{Speed}}=50.47-0.3503\text{Density}$.

Explanation of Solution

Calculation:

Linear regression model:

A linear regression model is given as$\widehat{y}=b_0+b_{1}x$ where $\widehat{y}$ is the predicted values of response variable and x is the predictor variable. The $b_1$ is the slope and $b_0$ is the intercept of the line.

Regression

Software procedure:

Step by step procedure to get the output using MINITAB software is given as,

• Choose Stat > Regression > Regression > Fit Regression Model.
• Under Responses, enter the column of Speed.
• Under predictors, enter the columns of Density.
• Click OK.

Output using MINITAB software is given below:

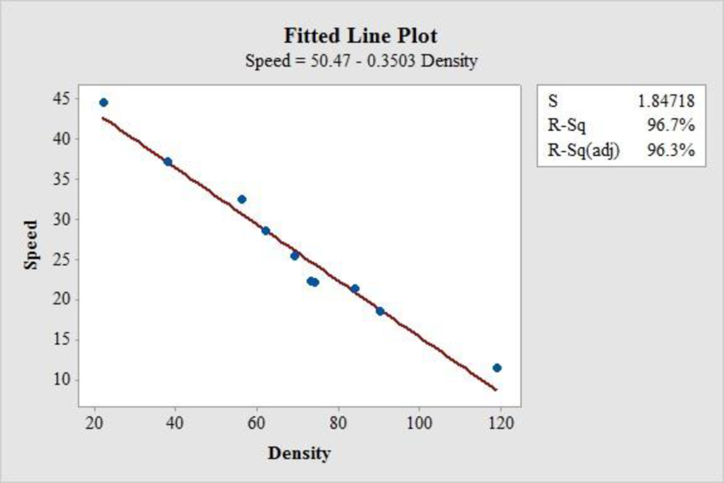
Thus, the regression equation of linear model is $\widehat{\text{Speed}}=50.47-0.3503\text{Density}$.

The fitted scatterplot of re-expressed data exhibits a linear pattern. Thus, there is a strong and negative linear association between speed and density of traffic.

$R^2$(R-squared):

The coefficient of determination ($R^2$) is defined as the proportion of variation in the observed values of the response variable that is explained by the regression.

In the given output, $\text{R squared}=96.7\%$

Thus, the 96.7% of the variability in speed is explained by density using linear regression model.

The conditions for a residual plot that is well fitted for the data are,

• There should not any bend, which would violate the straight line condition.
• There must not any outlier.
• There should not any change in the spread of the residuals from one part to another part of the plot.

Residual plot:

Software procedure:

Step by step procedure to get the output using MINITAB software is given as,

• Choose Stat > Regression > Regression > Fit Regression Model.
• Under Responses, enter the column of Speed.
• Under Continuous predictors, enter the columns of Density.
• In Graphs, under Residuals for plots choose Regular.
• Under Residuals plots choose Individuals plots and select box of Residuals versus fits.
• Click OK.

Output using MINITAB software is given below:

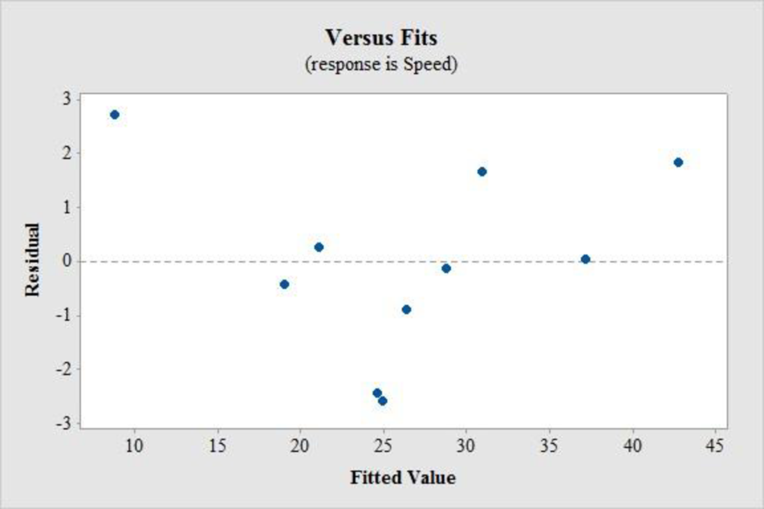
In residual plot, there is no bend or pattern, which can violate the straight line condition and there is no change in the spread of the residuals from one part to another part of the plot.

Thus, a linear model is appropriated.

c.

To determine

Find the residual of a traffic, having density and observed speed of 56 cars/mile and 32.5 mph, respectively.

Find the residual of another traffic, having density and observed speed of 20 cars/mile and 36.1 mph, respectively.

Answer to Problem 4E

The residual of a traffic, having density and observed speed of 56 cars/mile and 32.5 mph, respectively is 1.65 mph and the residual of a traffic, having density and observed speed of 20 cars/mile and 36.1 mph, respectively is –7.36 mph.

Explanation of Solution

Calculation:

Assume x be the predictor variable and y be the response variable, of a regression analysis. Then, the predicted value of the response variable is ${\widehat{y}}_p=b_0+b_1{x}_p$, where $x_p$is particular value of predictor variable x, $b_0$ is the y-intercept of the equation and $b_1$ is the slope of the equation.

Residual:

The residual is defined as $\text{Residual = Observed value }-\text{ Predicted value}$ or $e=y-\widehat{y}$ where $\widehat{y}$ be the predicted value of the response variable and y be the actual value of the response variable.

If the observed value is less than predicted value then the residual will be negative and if the observed value is greater than predicted value then the residual will be positive.

From the previous part b. it is found that the regression equation of linear model is $\widehat{\text{Speed}}=50.47-0.3503\text{Density}$.

The predicted speed of a traffic having density of 56 cars/mile is,

$\begin{array}{c}\widehat{\text{Speed}}=50.47-0.3503\left(56\right)\\ =50.47-19.6168\\ =30.8532\end{array}$

Thus, the predicted speed of a traffic having density of 56 cars/mile is 30.8532 mph.

It is known, that actual speed of a traffic having density of 56 cars/mile is 32.5 mph.

The value of the residual is,

$\begin{array}{c}e=\text{Speed}-\widehat{\text{Speed}}\\ =32.5-30.8532\\ \approx 1.65\end{array}$

Thus, the residual of a traffic, having density and observed speed of 56 cars/mile and 32.5 mph, respectively is 1.65 mph.

The predicted speed of a traffic having density of 20 cars/mile is,

$\begin{array}{c}\widehat{\text{Speed}}=50.47-0.3503\left(20\right)\\ =50.47-7.006\\ =43.46\end{array}$

Thus, the predicted speed of a traffic having density of 20 cars/mile is 43.46 mph.

It is known, that actual speed of a traffic having density of 20 cars/mile is 36.1 mph.

The value of the residual is,

$\begin{array}{c}e=\text{Speed}-\widehat{\text{Speed}}\\ =36.1-43.46\\ \approx -7.36\end{array}$

Thus, the residual of a traffic, having density and observed speed of 20 cars/mile and 36.1 mph, respectively is –7.36 mph.

d.

To determine

Find the unusual residual.

Answer to Problem 4E

Second residual is more unusual residual.

Explanation of Solution

From previous part c. it is found that residual of a traffic, having density and observed speed of 56 cars/mile and 32.5 mph, respectively is 1.65 mph and the residual of a traffic, having density and observed speed of 20 cars/mile and 36.1 mph, respectively is –7.36 mph.

Thus, it is clear that the second residual value is far away from the predicted value. Therefore, second residual is more unusual residual.

e.

To determine

Explain about slope and the correlation if the new point

$\left(\text{Density}=125\text{Cars/Mile,}\text{Speed}=55\text{mph}\right)$were included.

Explanation of Solution

The new point $\left(\text{Density}=125\text{Cars/Mile,}\text{Speed}=55\text{mph}\right)$ has a high density with a very high speed. Therefore, the inclusion of the point results in a very different regression analysis. The point has a high influence on the data. As a result of this the slope and correlation of the regression become weaker, close to 0.

In another words, shallower slope and weaker correlation are closer to 0 as they are both started as negative quantity.

Thus, technically slope and correlation becomes higher.

f.

To determine

Predict the speed of traffic for a density of 200 cars/mile.

Explain whether the prediction is reasonable.

Answer to Problem 4E

The predicted speed of a traffic having density of 200 cars/mile is –19.6 mph.

Explanation of Solution

Calculation:

The predicted speed of a traffic having density of 200 cars/mile is,

$\begin{array}{c}\widehat{\text{Speed}}=50.47-0.3503\left(200\right)\\ =50.47-70.06\\ \approx -19.6\end{array}$

Thus, the predicted speed of a traffic having density of 200 cars/mile is –19.6 mph.

This result is not meaningful as the value of the speed comes as negative quantity, which cannot be possible. Moreover, the given car density of 200 cars/mile is far beyond from the observed values.

Thus, the prediction is not reasonable.

g.

To determine

Find the equation to predict the standardized speed from the standardized density if both the variables are standardized.

Answer to Problem 4E

The equation to predict the standardized speed from the standardized density is $\widehat{z_{\text{Speed}}}=\left(-0.984\right)z_{\text{Density}}$.

Explanation of Solution

Calculation:

z-score:

The z-score of a random variable x is defined as $z=\frac{y-\mu }{\sigma }$, where $\mu$ be the mean of the random variable x and $\sigma$ be the standard deviation of the random variable x.

Correlation coefficient:

Software Procedure:

Step by step procedure to obtain the correlation coefficient of the data using the MINITAB software:

• Choose Stat > Basic Statistics > Correlation.
• In Variables, enter the column of Speed and Density.
• Click OK in all dialogue boxes.

Output using the MINITAB software is given below:

Thus, the correlation confident for speed and density is –0.984.

It is known that, the slope $b_1$of a regression line $\widehat{y}=b_0+b_{1}x$can be defined as,

$b_1=r\frac{s_y}{s_x}$, where r is the coefficient between predictor variable x and the response variable y. The $s_x$ and $s_y$ are the standard deviation of predictor variable x and the response variable y, respectively.

Now, for the predictor variable x and response variable y also scarify the regression equation $\overline{y}=b_0+b_1\overline{x}$.

Consider, the mean of the predictor variable x is $\overline{x}$and standard deviation is $s_x$. Similarly, the mean of the response variable y is $\overline{y}$and standard deviation is $s_y$.

Subtract the equation $\overline{y}=b_0+b_1\overline{x}$ from equation $\widehat{y}=b_0+b_{1}x$ it is found that,

$\widehat{y}-\overline{y}=b_1\left(x-\overline{x}\right)$

Using the formula $b_1=r\frac{s_y}{s_x}$ it is also found that,

$\begin{array}{c}\widehat{y}-\overline{y}=r\frac{s_y}{s_x}\left(x-\overline{x}\right)\\ \frac{\widehat{y}-\overline{y}}{s_y}=r\frac{\left(x-\overline{x}\right)}{s_x}\\ \widehat{z_y}=r{z}_x\end{array}$

In this problem, as speed is the predictor variable (x) and density of traffic is response variable (y) with the correlation coefficient of $r=-0.984$, then the equation to predict the standardized speed from the standardized density is $\widehat{z_{\text{Speed}}}=\left(-0.984\right)z_{\text{Density}}$.

h.

To determine

Find the equation to predict the standardized density from the standardized speed if both the variables are standardized.

Answer to Problem 4E

The equation to predict the standardized density from the standardized speed is $\widehat{z_{\text{Density}}}=\left(-0.984\right)z_{\text{Speed}}$.

Explanation of Solution

Calculation:

From the previous part g. it is found that the correlation confident for speed and density is –0.984. In addition correlation is same regardless of the direction of prediction.

Consider, the mean of the predictor variable x is $\overline{x}$and standard deviation is $s_x$. Similarly, the mean of the response variable y is $\overline{y}$and standard deviation is $s_y$.

Subtract the equation $\overline{y}=b_0+b_1\overline{x}$ from equation $\widehat{y}=b_0+b_{1}x$ it is found that,

$\widehat{y}-\overline{y}=b_1\left(x-\overline{x}\right)$

Using the formula $b_1=r\frac{s_y}{s_x}$ it is also found that,

$\begin{array}{c}\widehat{y}-\overline{y}=r\frac{s_y}{s_x}\left(x-\overline{x}\right)\\ \frac{\widehat{y}-\overline{y}}{s_y}=r\frac{\left(x-\overline{x}\right)}{s_x}\\ \widehat{z_y}=r{z}_x\end{array}$

In this problem, as density is the predictor variable (x) and speed of traffic is response variable (y) with the correlation coefficient of $r=-0.984$, then the equation to predict the standardized speed from the standardized density is $\widehat{z_{\text{Density}}}=\left(-0.984\right)z_{\text{Speed}}$.