10th Edition

ISBN: 9780135230008

Author: WEISS

Publisher: PEARSON

See similar textbooks

Videos

Textbook Question

Chapter C.1, Problem 14E

In each of Exercises C.11–C.17 identify the following:

a. the response, variable
b. the factors
c. the levels of each factor
d. the number of treatment combinations
e. the experimental units
f. the number of observations for each treatment combination
g. the experimental factors, if any
h. the classification factors, if any
i. whether the study is a designed experiment or an observational study

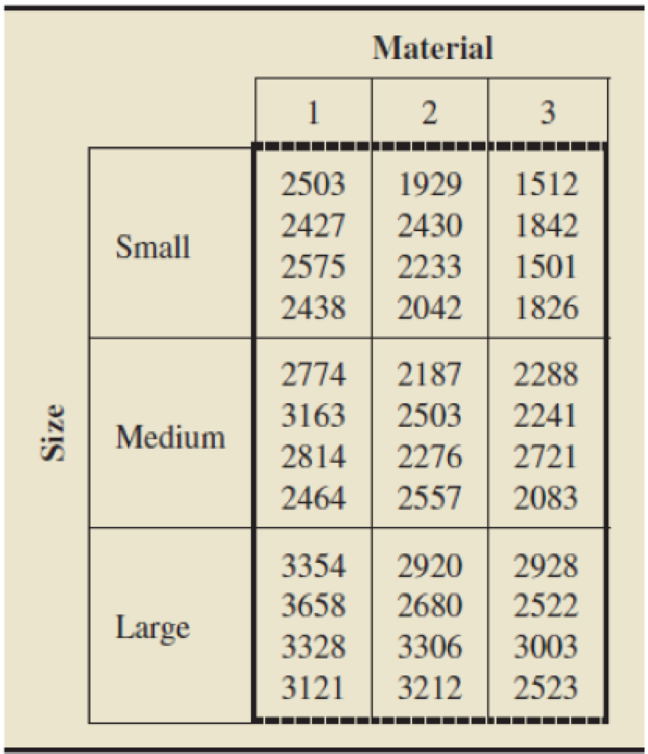
C.14 Highway Signs. A driver’s ability to detect highway signs is an important consideration in highway safety. In his dissertation Highway Construction Safety and the Aging Driver (1994), Solomon Younes investigated the distance at which drivers can first detect highway caution signs. This distance is called the detection distance. An experiment was conducted to determine the effects that sign size and sign material have on detection distance. Four drivers were randomly selected for each combination of sign size (small, medium, and large), and sign material (1, 2, and 3). Each driver covered the same stretch of highway at a constant speed during the same time of day, and the detection distance (in feet) was determined for the driver’s assigned caution sign. The data in the following table are based on the results of the experiment.

Chapter C.1, Problem 14E, In each of Exercises C.11C.17 identify the following: a. the response, variable b. the factors c.

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter C.1, Problem 13E

Chapter C.1, Problem 15E

Students have asked these similar questions

NC Current Students - North Ce X | NC Canvas Login Links - North ( X Final Exam Comprehensive x Cengage Learning x WASTAT - Final Exam - STAT → C webassign.net/web/Student/Assignment-Responses/submit?dep=36055360&tags=autosave#question3659890_9 Part (b) Draw a scatter plot of the ordered pairs. N Life Expectancy Life Expectancy 80 70 600 50 40 30 20 10 Year of 1950 1970 1990 2010 Birth O Life Expectancy Part (c) 800 70 60 50 40 30 20 10 1950 1970 1990 W ALT 林 $ # 4 R J7 Year of 2010 Birth F6 4+ 80 70 60 50 40 30 20 10 Year of 1950 1970 1990 2010 Birth Life Expectancy Ox 800 70 60 50 40 30 20 10 Year of 1950 1970 1990 2010 Birth hp P.B. KA & 7 80 % 5 H A B F10 711 N M K 744 PRT SC ALT CTRL

Harvard University California Institute of Technology Massachusetts Institute of Technology Stanford University Princeton University University of Cambridge University of Oxford University of California, Berkeley Imperial College London Yale University University of California, Los Angeles University of Chicago Johns Hopkins University Cornell University ETH Zurich University of Michigan University of Toronto Columbia University University of Pennsylvania Carnegie Mellon University University of Hong Kong University College London University of Washington Duke University Northwestern University University of Tokyo Georgia Institute of Technology Pohang University of Science and Technology University of California, Santa Barbara University of British Columbia University of North Carolina at Chapel Hill University of California, San Diego University of Illinois at Urbana-Champaign National University of Singapore McGill…

Name Harvard University California Institute of Technology Massachusetts Institute of Technology Stanford University Princeton University University of Cambridge University of Oxford University of California, Berkeley Imperial College London Yale University University of California, Los Angeles University of Chicago Johns Hopkins University Cornell University ETH Zurich University of Michigan University of Toronto Columbia University University of Pennsylvania Carnegie Mellon University University of Hong Kong University College London University of Washington Duke University Northwestern University University of Tokyo Georgia Institute of Technology Pohang University of Science and Technology University of California, Santa Barbara University of British Columbia University of North Carolina at Chapel Hill University of California, San Diego University of Illinois at Urbana-Champaign National University of Singapore…

Chapter C Solutions

INTRO.STATISTICS,TECH.UPDT.-W/MYSTATLAB

Ch. C.1 - Define the following terms: a. factor b. levels of...Ch. C.1 - A three-way factorial design has Factor A at 3...Ch. C.1 - A four-way factorial design has Factor A at 2...Ch. C.1 - A three-way factorial design has Factor A at 6...Ch. C.1 - Answer true or false to each of the following...Ch. C.1 - Prob. 8E Ch. C.1 - Answer true or false to each of the following...Ch. C.1 - Prob. 10E Ch. C.1 - In each of Exercises C.11C.17 identify the...Ch. C.1 - In each of Exercises C.11C.17 identify the...

Knowledge Booster

$Statistics$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Solution Summary: The author identifies the response variable, the detection distance, and the number of treatment combinations.

Videos

Want to see the full answer?

Chapter C Solutions