Calculus: An Applied Approach (MindTap Course List)
10th Edition
ISBN: 9781305860919
Author: Ron Larson
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter B, Problem 8E
To determine
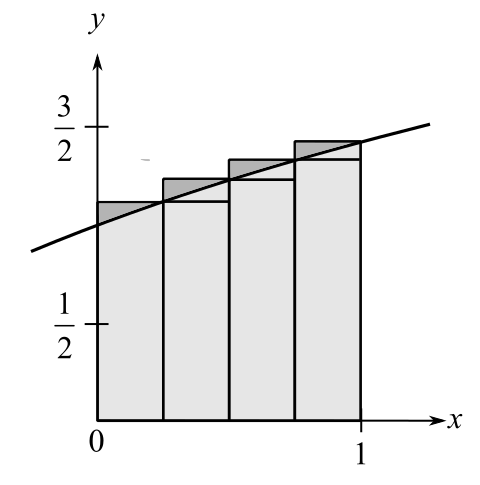
To calculate: The approximate area of the region lying between the graph of
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Can someone help me with this
Subject : calculas
(3) Showing all your working, find the solution set which describes the area shown in green
below.
과
Chapter B Solutions
Calculus: An Applied Approach (MindTap Course List)
Ch. B - Using Rectangles to Approximate the Area of a...Ch. B - Prob. 2ECh. B - Prob. 3ECh. B - Prob. 4ECh. B - Prob. 5ECh. B - Prob. 6ECh. B - Prob. 7ECh. B - Prob. 8ECh. B - Comparing Riemann Sums Consider a triangle of area...Ch. B - Comparing Riemann Sums Consider a trapezoid of...
Ch. B - Writing a Definite Integral In Exercises 1118, set...Ch. B - Writing a Definite Integral In Exercises 11-18,...Ch. B - Writing a Definite Integral In Exercises 1118, set...Ch. B - Prob. 14ECh. B - Writing a Definite Integral In Exercises 1118, set...Ch. B - Prob. 16ECh. B - Prob. 17ECh. B - Writing a Definite Integral In Exercises 11-18,...Ch. B - Prob. 19ECh. B - Prob. 20ECh. B - Prob. 21ECh. B - Prob. 22ECh. B - Prob. 23ECh. B - Prob. 24ECh. B - Prob. 25ECh. B - Prob. 26ECh. B - Prob. 27ECh. B - Finding Areas of Common Geometric Figures In...Ch. B - Prob. 29ECh. B - Prob. 30ECh. B - Prob. 31ECh. B - Prob. 32E
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- pts) A pneumotachograph is a medical device used to measure the rate at which air is haled by a patient's lungs. Suppose Figure 1, below, shows the rate of exhalation for a rticular patient. The area under the graph provides a measure of the total volume of air the lungs during exhalation. Use a Riemann sum with four rectangles and midpoint of ch subinterval as the height to estimate the volume of air exhaled from the patients lungs 2.4 seconds. flow rate 1 0.75 + 0.5 0.25 time 0.6 1.2 1.8 2.4 Seconds FIGURE 1. Rate of exhalation. Liters/secondarrow_forwardFind shaded area ? 8.1)arrow_forwardQuiz 5.4 (Fundamental Theore X A webassign.net/web/Student/Assignment-Responses/submit?pos3D48&de MY NOTES ASK YOUR TEACHER Find the area of the region. 5. y = 5- 4 1. 10 15 20 25 -1F Submit Answer 3. 2.arrow_forward
- Current Attempt in Progress Write a Riemann sum and then a definite integral representing the volume of the region, using the slice shown. Evaluate the integral exactly. NOTE: Enter the exact value or round to three decimal places. Volume= The volume of the region is dx 6 cm Ax 4 cmarrow_forwardThe rectangles in the graph below illustrate a left endpoint Riemann sum for f(x)= (13/x) on the interval [2, 6]. The value of this left endpoint Riemann sum is and this Riemann sum is [select an answer] v the area of the region enclosed by y = f(x), the x-axis, and the vertical lines x = 2 and x = 6. 8 7 5 2 1 1 2 3 4 5 7 8 Left endpoint Riemann sum for y = (13/x) on [2, 6]arrow_forwardSpeedometer readings for a vehicle (in motion) at 3-second intervals are given in the table. t (sec) 0 3 6 9 12 15 18 10 34 60 77 74 54 v (ft/s) 0 Estimate the distance traveled by the vehicle during this 18-second period using a left sum Lå, a right sum R6, and a middle sum M3. L6 = R6 = M3 = feet feet feetarrow_forward
- Sketch the region enclosed by the curves. x+y= 5, y+3x = 5, x- y=0 f(x) = x+y=5,y+3x=5,x-y=0 poweresby desma Compute the area A of the region as an integral along the x- or y-axis. (Give an exact answer. Use symbolic notation and fractions where needed.) 125 A = 16 +arrow_forwardSolve (help)arrow_forwardTo use Cavalier's Principle, we divide a figure into familiar shapes to determine the total area or volume of the original shape. Thus Cavalier's Principle is a strategy that can be used for approximating the _______ and ______ of an irregularly shaped figure.arrow_forward
- Learning Target INT2: I can calculate the area between curves, net change, and displacement using geometric for- mulas and Riemann sums. Consider the function f(x) = cos z. Estimate the area under the curve, above the r axis and between x = 0 and = 7 using the following Riemann sums. On each part, clearly state the value of Ax, clearly state which points (on a graph, for example) you are using for rectangles, and show the setup of the calculation. You are encouraged to use a spreadsheet or WolframAlpha to do the actual calculation. Keep the approximations to 4 decimal places. 1. Sketch the curve and draw approximating rectangles 2. left-endpoint approximation, n = 4 3. right endpoint endpoint approximation, n = 4arrow_forwardPlease show work thank you!arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Numerical Integration Introduction l Trapezoidal Rule Simpson's 1/3 Rule l Simpson's 3/8 l GATE 2021; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=zadUB3NwFtQ;License: Standard YouTube License, CC-BY