
To show that any tree is 2-colorable.
Explanation of Solution
Given Information:
A 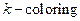 of an undirected graph
of an undirected graph 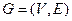 is a function
is a function 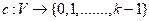 such that
such that 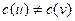 for every edge
for every edge 
Explanation:
There are no loops in tree, if a color (0) is given to a node, then all its neighbors should be colored with a different color say color (1). Now color the neighbors of all these neighbors with color (0). In this way keep coloring alternating colors until the whole tree is colored. Since there are no loops no node will be visited and thus colored twice. In the end any path in the tree has vertices with alternating colors.
To show that the following are equivalent:
- G is bipartite.
- G is 2-colorable.
- G has no cycles of odd length.
Explanation of Solution
A bipartite graph has two sets of vertices which has equal number of vertices in those two sets. So, if the given graph G is bipartite that means it will be 2 colorable because one set of vertices can be colored with one color say color (0) and another set of vertices can be colored with another set of vertices say color (1).
The following figure shows the bipartite graph with chromatic number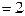
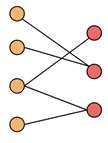
Also, it can be seen that it has no cycles of odd length from the above figure of bipartite graph.
So, on the basis of above illustration- the following points can be made-
- G is bipartite.
- G is 2-colorable.
- G has no cycles of odd length.
To prove that a Graph can be colored with 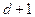 colors where
colors where 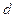 is the maximum degree of any vertex in graph.
is the maximum degree of any vertex in graph.
Explanation of Solution
Greedy coloring procedure requires us to number the colorsthat are used. So, each time a new color is introduced it is numbered.
Greedy coloring
If the maximum degree vertex of a graph has degree d, let this vertex be v.
Color v with color 1.
Since all the adjacent vertices of 'v' have to be colored with a color other than color of 'v', let us assume that all the adjacent vertices are colored with different colors.
As number of neighbors is d, hence number of additional colors required is d. So, maximum d+1 colors are needed.
This is the maximum number of colors needed because in no case there will be more than d+1 colorsas the maximum degree is d. (All the neighbors and other nodes of graph have degree <= d)
Proof by mathematical induction:
Base case: A graph with just 1 vertex has maximum degree 0 and needs only 1 color. It is 1-colorable.
Inductive hypothesis: It can be assumed that any graph which has = k vertices and maximum vertex degree = d can be colored with d+1 colors.
Inductive Step: Now suppose there is a graph G with k+1 vertices and maximum degree d. Remove a vertex v (and all its edges) from G to create a smaller graph G'.
The maximum degree of G' is not greater than d, because removing a vertex from G' won't increase its degree. So, by the inductive hypothesis, G' can be colored with d + 1 colors. The neighbors of v are only using d of the available colors because v has maximum d neighbors, leaving a spare color that can be assigned to v.
Therefore, the coloring of G is an extension of coloring of G'. Hence, G can be colored with d+1 colors. G is (d+1)-colorable.
To show that a graph G can be colored with 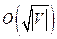 if it has
if it has 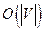 edges.
edges.
Explanation of Solution
Run the above greedy algorithm when a color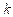 is used for the first time, to color a vetex
is used for the first time, to color a vetex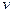 mark the edges joining
mark the edges joining 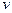 to vertices already coloured which is atleast
to vertices already coloured which is atleast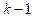
Every marked edge is marked only once during the process and at least 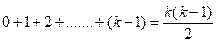 edges will be marked when number of colors are used. So if number of colors are present, then number of edges will be colored.
edges will be marked when number of colors are used. So if number of colors are present, then number of edges will be colored. 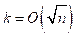
Want to see more full solutions like this?
Chapter B Solutions
Introduction To Algorithms, Third Edition (international Edition)
- Node.js, Express.js, MongoDB, and Mongoose: Create, Read, Update, and Delete Operations There is a program similar to this assignment given as the last example, CRUD, in the lecture notes for the week that discusses the introduction to MongoDB. Basically, you need to adapt this example program to the data given in this assignment. This program will take more time that previous assignments. So, hopefully you'll start early and you've kept to the schedule in terms of reading the lecture notes. You can use compass if you want to create this database. Or, when your connection string in the model runs it will create the database for you if one does not yet exist. So, ⚫ create a Mongoose model based on the info given below. The index.html page is given in the same folder as these notes. • When you successfully run index.js and instantiate the model, your database is created. • Once the database is created, you need to perfect the addCar route so you can add data using the index.html page. •…arrow_forward1. Enabled with SSL, HTTPS protocol is widely used to provide secure Web services to Web users using Web browsers on the Internet. How is a secure communication channel established at the start of communication between a Web server running HTTPS and a Web browser? Consider the following threats to Web security and how each of these threats is countered by a particular feature of SSL. Man-in-the-middle attack: An attacker interposes during key exchange, acting as the client to the server and as the server to the client. Password sniffing: Passwords in HTTP or other application traffic are “eavesdropped.” SYN flooding: An attacker sends TCP SYN messages to request a connection but does not respond to the final message to establish the connection fully. The attacked TCP module typically leaves the “half-open” connection around for a few minutes. Repeated SYN messages can clog the TCP module.arrow_forwardSQL Injection on UPDATE Statement for educational purpose only Based on the information below how do i update this code in order to update the emplyees field, eg admin nickname, email,address, phone number etc? ' ; UPDATE users SET NickName='Hacked' WHERE role='admin' -- If a SQL injection vulnerability happens to an UPDATE statement, the damage will be more severe, because attackers can use the vulnerability to modify databases. In our Employee Management application, there is an Edit Profile page (Figure 2) that allows employees to update their profile information, including nickname, email, address, phone number, and password. To go to this page, employees need to log in first. When employees update their information through the Edit Profile page, the following SQL UPDATE query will be executed. The PHP code implemented in unsafe edit backend.php file is used to update employee’s profile information. The PHP file is located in the /var/www/SQLInjection directory.arrow_forward
 Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole Fundamentals of Information SystemsComputer ScienceISBN:9781305082168Author:Ralph Stair, George ReynoldsPublisher:Cengage Learning
Fundamentals of Information SystemsComputer ScienceISBN:9781305082168Author:Ralph Stair, George ReynoldsPublisher:Cengage Learning C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning Principles of Information Systems (MindTap Course...Computer ScienceISBN:9781285867168Author:Ralph Stair, George ReynoldsPublisher:Cengage Learning
Principles of Information Systems (MindTap Course...Computer ScienceISBN:9781285867168Author:Ralph Stair, George ReynoldsPublisher:Cengage Learning New Perspectives on HTML5, CSS3, and JavaScriptComputer ScienceISBN:9781305503922Author:Patrick M. CareyPublisher:Cengage Learning
New Perspectives on HTML5, CSS3, and JavaScriptComputer ScienceISBN:9781305503922Author:Patrick M. CareyPublisher:Cengage Learning





