To show that any tree is 2-colorable.
Explanation of Solution
Given Information:
A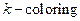 
of an undirected graph 
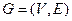is a function 
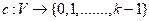such that 
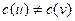for every edge 
Explanation:
There are no loops in tree, if a color (0) is given to a node, then all its neighbors should be colored with a different color say color (1). Now color the neighbors of all these neighbors with color (0). In this way keep coloring alternating colors until the whole tree is colored. Since there are no loops no node will be visited and thus colored twice. In the end any path in the tree has vertices with alternating colors.
To show that the following are equivalent:
- G is bipartite.
- G is 2-colorable.
- G has no cycles of odd length.
Explanation of Solution
A bipartite graph has two sets of vertices which has equal number of vertices in those two sets. So, if the given graph G is bipartite that means it will be 2 colorable because one set of vertices can be colored with one color say color (0) and another set of vertices can be colored with another set of vertices say color (1).
The following figure shows the bipartite graph with chromatic number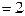
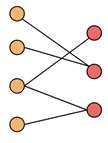
Also, it can be seen that it has no cycles of odd length from the above figure of bipartite graph.
So, on the basis of above illustration- the following points can be made-
- G is bipartite.
- G is 2-colorable.
- G has no cycles of odd length.
To prove that a Graph can be colored with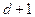 
colors where 
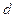is the maximum degree of any vertex in graph.
Explanation of Solution
Greedy coloring procedure requires us to number the colorsthat are used. So, each time a new color is introduced it is numbered.
Greedy coloring
If the maximum degree vertex of a graph has degree d, let this vertex be v.
Color v with color 1.
Since all the adjacent vertices of 'v' have to be colored with a color other than color of 'v', let us assume that all the adjacent vertices are colored with different colors.
As number of neighbors is d, hence number of additional colors required is d. So, maximum d+1 colors are needed.
This is the maximum number of colors needed because in no case there will be more than d+1 colorsas the maximum degree is d. (All the neighbors and other nodes of graph have degree <= d)
Proof by mathematical induction:
Base case: A graph with just 1 vertex has maximum degree 0 and needs only 1 color. It is 1-colorable.
Inductive hypothesis: It can be assumed that any graph which has = k vertices and maximum vertex degree = d can be colored with d+1 colors.
Inductive Step: Now suppose there is a graph G with k+1 vertices and maximum degree d. Remove a vertex v (and all its edges) from G to create a smaller graph G'.
The maximum degree of G' is not greater than d, because removing a vertex from G' won't increase its degree. So, by the inductive hypothesis, G' can be colored with d + 1 colors. The neighbors of v are only using d of the available colors because v has maximum d neighbors, leaving a spare color that can be assigned to v.
Therefore, the coloring of G is an extension of coloring of G'. Hence, G can be colored with d+1 colors. G is (d+1)-colorable.
To show that a graph G can be colored with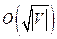 
if it has 
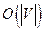edges.
Explanation of Solution
Run the above greedy algorithm when a color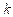
is used for the first time, to color a vetex
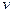mark the edges joining 
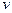to vertices already coloured which is atleast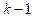
Every marked edge is marked only once during the process and at least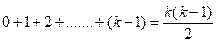 
edges will be marked when number of colors are used. So if number of colors are present, then number of edges will be colored.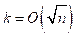 
Want to see more full solutions like this?
Chapter B Solutions
Introduction to Algorithms
- #include <stdio.h>int main(void) {int a;char *s;int v0 = 4, v1 = 5, v2 = 6, v3 = 1, v4 = 2;printf("Exercise 1:\n====================\n");switch(v0) {case 0: printf("Hello October\n"); break;case 1: printf("Go Kean!\n"); break;case 2: printf("Academic Building Center \n"); break;case 3: printf("UNION \n"); break;case 4: printf("Go ");case 5: printf("Kean! \n");default: printf("Have a great semester! \n"); break;}for(a=5; a<v1; a++) {printf("Kean");}printf("\n");if (v2 == 6) {s = "Go";}else {s = "Hello";}if(v3 != v4) {printf("%s Kean!\n",s);} else {printf("%s Computer Science!\n",s);}return 0;} Output: Exercise 1:====================Go Kean! Have a great semester! Go Kean! Please only modify the initial value of v0, v1, v2, v3 and v4 to get the following output. Youneed to show your program output (in the screenshot) and submit the code that youmodified.Exercise 1:====================Hello OctoberKeanHello Computer Science!arrow_forward(OnlineGDB) 1. Please read and run the following code and answer the questions.#include <stdio.h>int main(void) {int a;char *s;int v0 = 4, v1 = 5, v2 = 6, v3 = 1, v4 = 2;printf("Exercise 1:\n====================\n");switch(v0) {case 0: printf("Hello October\n"); break;case 1: printf("Go Kean!\n"); break;case 2: printf("Academic Building Center \n"); break;case 3: printf("UNION \n"); break;case 4: printf("Go ");case 5: printf("Kean! \n");default: printf("Have a great semester! \n"); break;}for(a=5; a<v1; a++) {printf("Kean");}printf("\n");if (v2 == 6) {s = "Go";}else {s = "Hello";}if(v3 != v4) {printf("%s Kean!\n",s);} else {printf("%s Computer Science!\n",s);}return 0;} What is the output of the program? Please explain why.arrow_forward1.[30 pts] Answer the following questions: a. [10 pts] Write a Boolean equation in sum-of-products canonical form for the truth table shown below: A B C Y 0 0 0 1 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 1 1 1 1 0 a. [10 pts] Minimize the Boolean equation you obtained in (a). b. [10 pts] Implement, using Logisim, the simplified logic circuit. Include an image of the circuitarrow_forward
- In the past, encryption and decryption were mostly done by substitution and permutation of letters in a text message. study those classic cryptographic schemes Then, develop an automatic cipher using Javascript The cipher should be able to perform the following tasks: generate keys encrypt a given plaintext message with a key selected from the list of keys generated decrypt a given ciphertext message with a known cipher keyarrow_forwardList reasons why teachers should and shouldn’t be replaced by computers? State your response in a descriptive context. Provide five references from the with internet with your answers.arrow_forwardThe attached picture shows the RTCAPI memory mapped register which has the address 0x180. 1) Program the MCU's registers so that a) SIRC is the clock source b) the clock is divided by 16K c) the clock is enabled d) load is enabledarrow_forward
- What is the ALU result if the 4-bit ALU Control signal is 0100? What happens if the ALU Control signal is 0101?arrow_forwardIn the past, encryption and decryption were mostly done by substitution and permutation of letters in a text message. study those classic cryptographic schemes Then, develop an automatic cipher using a programming language of your choice. The cipher should be able to perform the following tasks: generate keys encrypt a given plaintext message with a key selected from the list of keys generated decrypt a given ciphertext message with a known cipher keyarrow_forwardCase Study Instructions: Offshore Wind Energy in the North Sea For this case study, students will analyze the institutional challenges and social rules surrounding offshore wind energy development in the Dutch North Sea, as explored in the case study from the textbook (pages 44-46). Additional resources in this week’s learning module will provide further perspectives on the impact of wind energy on different stakeholders. Students should refer to the syllabus for specific guidelines regarding length, format, and content requirements. Reflection Questions to Consider: What are the key institutional challenges in implementing offshore wind energy in the North Sea? How do formal and informal social rules shape the use of this shared space? What conflicts arise between different stakeholders (e.g., fishermen, naval transport, military, and wind energy developers)? How can policymakers balance economic, environmental, and social considerations when allocating space for wind energy?…arrow_forward
- Alphabetic Telephone Number TranslatorMany companies use telephone numbers like 555-GET-FOOD so the number is easier for their customers to remember. On a standard telephone, the alphabetic letters are mapped to numbers in the following fashion: A, B, and C = 2 D, E, and F = 3 G, H, and I = 4 J, K, and L = 5 M, N, and O = 6 P, Q, R, and S = 7 T, U, and V = 8 W, X, Y, and Z = 9 Write a program that asks the user to enter a 10-character telephone number in the format XXX-XXX-XXXX. The application should display the telephone number with any alphabetic characters that appeared in the original translated to their numeric equivalent. For example, if the user enters 555-GET-FOOD, the application should display 555-438-3663.arrow_forwardI would like help to resolve the following casearrow_forward7. Character AnalysisIf you have downloaded the source code you will find a file named text.txt in the Chapter 08 folder. Write a program that reads the file’s contents and determines the following: The number of uppercase letters in the file The number of lowercase letters in the file The number of digits in the file The number of whitespace characters in the filearrow_forward
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole
Fundamentals of Information SystemsComputer ScienceISBN:9781305082168Author:Ralph Stair, George ReynoldsPublisher:Cengage Learning
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
Principles of Information Systems (MindTap Course...Computer ScienceISBN:9781285867168Author:Ralph Stair, George ReynoldsPublisher:Cengage Learning
New Perspectives on HTML5, CSS3, and JavaScriptComputer ScienceISBN:9781305503922Author:Patrick M. CareyPublisher:Cengage Learning