
Concept explainers
(a)
Plot the data and the regression line on the same axes. Does the line fit the data well?
(a)
Answer to Problem 1P
Yes, the line fits the data well
Explanation of Solution
Given information:
Table gives the gross world product, G, which measures output of goods and services. If t is in years since 1950, the regression line these data is
G in tillions of 1999 dollars.
| Year | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 |
| G | 6.4 | 10.0 | 16.3 | 23.6 | 31.9 | 43.2 |
Calculation:
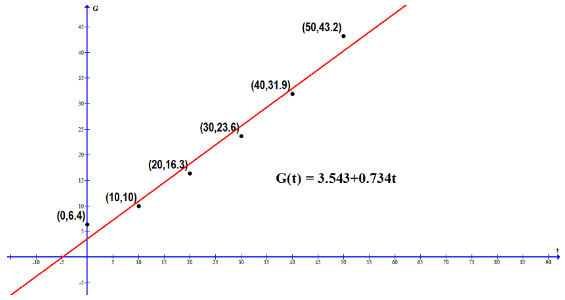
Yes, the line fits the data well (is in fact the linear regression line) with
(b)
Interpret the slope of the line in terms of gross world product.
(b)
Explanation of Solution
The gross world product, G, which measures global output of goods and services is given by
Hence, the slope of G ( t ) indicates that gross world product increases by 0.734 trillion dollars every year.
(c)
Use the regression line to estimate gross world product in 2005 and in 2020. Comment on your confidence in the two predictions.
(c)
Answer to Problem 1P
The gross world product in 2005 = 1475.213 trillion dollars
The gross world product in 2020 = 1486.223 trillion dollars
Both predictions cannot be made confidently.
Explanation of Solution
Given information:
Table A.5 gives the gross world product, G, which measures output of goods and services. If t is in years since 1950, the regression line these data is
| Year | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 |
| G | 6.4 | 10.0 | 16.3 | 23.6 | 31.9 | 43.2 |
Calculation:
The gross world product, G, which measures global output of goods and services is given by
Both predictions cannot be made confidently because:
- Uniform increase in gross world product every year is highly unlikely in actual scenario.
- A recession (for example the one in 2009) can also lead to decrease in gross world product.
Thus, the gross world product in 2005 = 1475.213 trillion dollars
The gross world product in 2020 = 1486.223 trillion dollars
Both predictions cannot be made confidently.
Want to see more full solutions like this?
Chapter A Solutions
Applied Calculus, 6e WileyPLUS + Loose-leaf
- Evaluate the next integralarrow_forward1. For each of the following, find the critical numbers of f, the intervals on which f is increasing or decreasing, and the relative maximum and minimum values of f. (a) f(x) = x² - 2x²+3 (b) f(x) = (x+1)5-5x-2 (c) f(x) = x2 x-9 2. For each of the following, find the intervals on which f is concave upward or downward and the inflection points of f. (a) f(x) = x - 2x²+3 (b) g(x) = x³- x (c) f(x)=x-6x3 + x-8 3. Find the relative maximum and minimum values of the following functions by using the Second Derivative Test. (a) f(x)=1+3x² - 2x3 (b) g(x) = 2x3 + 3x² - 12x-4arrow_forwardFind the Soultion to the following dy differential equation using Fourier in transforms: = , хуо, ухо according to the terms: lim u(x,y) = 0 x18 lim 4x (x,y) = 0 x14 2 u (x, 0) = =\u(o,y) = -y لوarrow_forward
- Can you solve question 3,4,5 and 6 for this questionarrow_forwardwater at a rate of 2 m³/min. of the water height in this tank? 16) A box with a square base and an open top must have a volume of 256 cubic inches. Find the dimensions of the box that will minimize the amount of material used (the surface area). 17) A farmer wishes toarrow_forward#14 Sand pours from a chute and forms a conical pile whose height is always equal to its base diameter. The height o the pile increases at a rate of 5 feet/hour. Find the rate of change of the volume of the sand in the conical pile when the height of the pile is 4 feet.arrow_forward
- (d)(65in(x)-5 cos(x) dx mins by 5x-2x² 3x+1 dx -dx 20 Evaluate each the following indefinite integralsarrow_forward19 Evaluate each the following definite integrals: a) લ b) (+3) 6) (2-2)(+33) dxarrow_forward#11 If a snowball melts so its surface area decreases at a rate of 1cm²/min, find the rate at which the diameter decreases when the diameter is 6 cm.arrow_forward
- Use Deritivitve of the inverse to solve thisarrow_forwardEvaluate the following Limits: e6x-1 Lim +0Sin3x 7x-5x2 2x-1+ Cos 4x +6 c) Lim b) Lim + x³-x2 X-0 1-e' 4x d) Lim 6x²-3 X+0 6x+2x² Find the derivatives of the following functions using the Limit definition of derivativearrow_forward15A cylindrical tank with radius 8 m is being filled with water at a rate of 2 m³/min. What is the rate of change of the water height in this tank? 6)A box with a square base and an open top must box that will minimiarrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning





