Concept explainers
Videos
(a)
Plot the data and the regression line on the same axes. Does the line fit the data well?
(a)
Answer to Problem 1P
Yes, the line fits the data well
Explanation of Solution
Given information:
Table gives the gross world product, G, which measures output of goods and services. If t is in years since 1950, the regression line these data is
G in tillions of 1999 dollars.
| Year | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 |
| G | 6.4 | 10.0 | 16.3 | 23.6 | 31.9 | 43.2 |
Calculation:
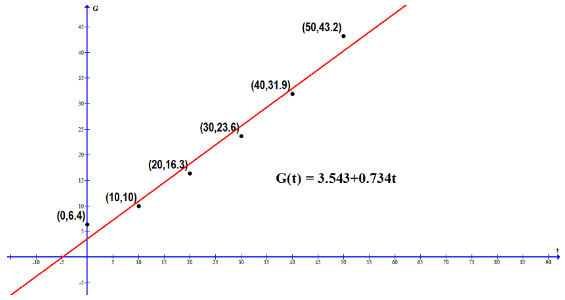
Yes, the line fits the data well (is in fact the linear regression line) with
(b)
Interpret the slope of the line in terms of gross world product.
(b)
Explanation of Solution
The gross world product, G, which measures global output of goods and services is given by
Hence, the slope of G ( t ) indicates that gross world product increases by 0.734 trillion dollars every year.
(c)
Use the regression line to estimate gross world product in 2005 and in 2020. Comment on your confidence in the two predictions.
(c)
Answer to Problem 1P
The gross world product in 2005 = 1475.213 trillion dollars
The gross world product in 2020 = 1486.223 trillion dollars
Both predictions cannot be made confidently.
Explanation of Solution
Given information:
Table A.5 gives the gross world product, G, which measures output of goods and services. If t is in years since 1950, the regression line these data is
| Year | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 |
| G | 6.4 | 10.0 | 16.3 | 23.6 | 31.9 | 43.2 |
Calculation:
The gross world product, G, which measures global output of goods and services is given by
Both predictions cannot be made confidently because:
- Uniform increase in gross world product every year is highly unlikely in actual scenario.
- A recession (for example the one in 2009) can also lead to decrease in gross world product.
Thus, the gross world product in 2005 = 1475.213 trillion dollars
The gross world product in 2020 = 1486.223 trillion dollars
Both predictions cannot be made confidently.
Want to see more full solutions like this?
Chapter A Solutions
APPLIED CALCULUS (WILEY PLUS)
- Q5. Briefly explain what are isotopes of an elements, with an example, and why some isotopes are radioactive. 470arrow_forwardQ1. Will you earn more interest amount in two years by depositing $2000 in a simple interest account that pays 6% or in an account that pays 6.15% interest compounded monthly? tarrow_forwardQ4. We want to invest $18000 in an account compounded continuously. How long should the investment be kept so final value of the account reaches $25000 if the annual rate of interest is 5.8%?arrow_forward
- Q3. Determine the effective annual yield for each investment below. Then select the better investment. Assume 365 days in a year. a) 5.6% compounded semiannually; b) 5.4% compounded daily.arrow_forwardQ2. You deposit $22,000 in an account that pays 4.8% interest compounded monthly. a. Find the future value after six years. & b b. Determine the effective annual yield of this account.arrow_forward18. Using the method of variation of parameter, a particular solution to y′′ + 16y = 4 sec(4t) isyp(t) = u1(t) cos(4t) + u2(t) sin(4t). Then u2(t) is equal toA. 1 B. t C. ln | sin 4t| D. ln | cos 4t| E. sec(4t)arrow_forward
- Question 4. Suppose you need to know an equation of the tangent plane to a surface S at the point P(2, 1, 3). You don't have an equation for S but you know that the curves r1(t) = (2 + 3t, 1 — t², 3 − 4t + t²) r2(u) = (1 + u², 2u³ − 1, 2u + 1) both lie on S. (a) Check that both r₁ and r2 pass through the point P. 1 (b) Give the expression of the 074 in two ways Ət ⚫ in terms of 32 and 33 using the chain rule მყ ⚫ in terms of t using the expression of z(t) in the curve r1 (c) Similarly, give the expression of the 22 in two ways Əz ди ⚫ in terms of oz and oz using the chain rule Əz მყ • in terms of u using the expression of z(u) in the curve r2 (d) Deduce the partial derivative 32 and 33 at the point P and the equation of მე მყ the tangent planearrow_forwardCoast Guard Patrol Search Mission The pilot of a Coast Guard patrol aircraft on a search mission had just spotted a disabled fishing trawler and decided to go in for a closer look. Flying in a straight line at a constant altitude of 1000 ft and at a steady speed of 256 ft/s, the aircraft passed directly over the trawler. How fast (in ft/s) was the aircraft receding from the trawler when it was 1400 ft from the trawler? (Round your answer to one decimal places.) 1000 ft 180 × ft/s Need Help? Read It SUBMIT ANSWERarrow_forward6. The largest interval in which the solution of (cos t)y′′ +t^2y′ − (5/t)y = e^t/(t−3) , y(1) = 2, y′(1) = 0is guaranteed to exist by the Existence and Uniqueness Theorem is:A. (0, ∞) B. (π/2, 3) C. (0,π/2) D. (0, π) E. (0, 3)arrow_forward
- 12. For the differential equation in the previous question, what is the correct form for a particularsolution?A. yp = Ae^t + Bt^2 B. yp = Ae^t + Bt^2 + Ct + DC. yp = Ate^t + Bt^2 D. yp = Ate^t + Bt^2 + Ct + D Previous differential equation y′′ − 4y′ + 3y = e^t + t^2arrow_forward16. The appropriate form for the particular solution yp(x) of y^(3) − y′′ − 2y′ = x^2 + e^2x isA. yp(x) = Ax^2 + Bx + C + De^2x B. yp(x) = Ax^3 + Bx^2 + Cx + Dxe^2xC. yp(x) = Ax^2 +Be^2x D. yp(x) = A+Be^2x +Ce^−x E. yp(x) = Ax^2 +Bx+C +(Dx+E)e^2xarrow_forwardDistance Between Two Ships Two ships leave the same port at noon. Ship A sails north at 17 mph, and ship B sails east at 11 mph. How fast is the distance between them changing at 1 p.m.? (Round your answer to one decimal place.) 20.3 X mph Need Help? Read It Watch It SUBMIT ANSWERarrow_forward
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning