
| In Exercises 1-6, do the following: | |
| a. | Determine the number of vertices edges, and loops in the given graph |
| b. | Draw another representation of the graph that looks significantly different. |
| c. | Find two adjacent edges. |
| d. | Find two adjacent vertices |
| e. | Find the degree of each vertex. |
| f. | Determine whether the graph is connected. |
 |
|
a)
The number of vertices, edges, and loops in the given graph.
Answer to Problem 1CR
Solution:
The number of vertices are
Explanation of Solution
Given:
The following figure shows the given diagram.
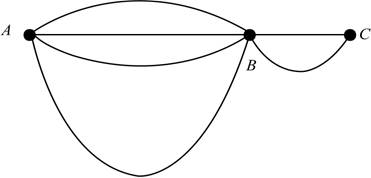
Figure
Approach:
A graph is the diagram that consists of points, known as vertices, and connecting lines are known as edges. The edge that connects a vertex with itself is called a loop.
Therefore, the number of vertices are
Conclusion:
Hence, the number of vertices are
b)
To draw:
The representation of the graph that looks significantly different.
Answer to Problem 1CR
Solution:
The representation of the graph that looks significantly different is shown in figure
Explanation of Solution
Approach:
The significantly different representation is as follows,
Take three vertices as A, B and C. Connect A and B with two edges, A and C with two edges. Make an edge between B and C. To form a loop make an edge that connects the vertex B with each other as shown below.
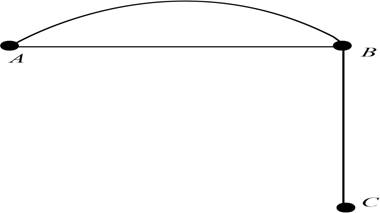
Figure
Therefore, the representation of the graph that looks significantly different is shown in figure
Conclusion:
Hence, the representation of the graph that looks significantly different is shown in figure
c)
To find:
The two adjacent edges of the given figure.
Answer to Problem 1CR
Solution:
The adjacent sides are AB, BC.
Explanation of Solution
Approach:
Adjacent edges are the edges which have a common vertex.
In the above given figure the adjacent sides are AB, BC.
Therefore, the adjacent sides are AB, BC.
Conclusion:
Hence, the adjacent sides are AB, BC.
d)
To find:
The two adjacent vertices.
Answer to Problem 1CR
Solution:
The vertices A and B, B and C are two adjacent vertices.
Explanation of Solution
Approach:
Two vertices will be adjacent if they are joined by an edge.
Thus in the above given figure Vertices A and B, B and C are two adjacent vertices.
Therefore, the vertices A and B, B and C are two adjacent vertices.
Conclusion:
Hence, the vertices A and B, B and C are two adjacent vertices.
e)
To find:
The degree of each vertex.
Answer to Problem 1CR
Solution:
The degree of each vertex is shown in the table (1).
Explanation of Solution
Approach:
The degree of vertex is defined as the total number of edges that are connected to it.
The degree of vertex is shown in the following table.
| Vertex | Degree |
| A | |
| B | |
| C |
Table (1)
Therefore, the degree of each vertex is shown in the table (1).
Conclusion:
Hence, the degree of each vertex is shown in the table (1).
f)
Whether the graph is connected or not.
Answer to Problem 1CR
Solution:
The given graph is said to be connected.
Explanation of Solution
Approach:
A graph will be connected if every pair of vertices in the graph is connected by a trail. A trail is sequence of adjacent vertices and the distinct edges that connect to them. Consider the above graph. There is a trail of
Therefore, the given graph is said to be connected.
Conclusion:
Hence, the given graph is said to be connected.
Want to see more full solutions like this?
Chapter 9 Solutions
MATHEMATICS A PRACTICAL ODYSSEY W/ACCESS
- Find a plane containing the point (3, -3, 1) and the line of intersection of the planes 2x + 3y - 3z = 14 and -3x - y + z = −21. The equation of the plane is:arrow_forwardDetermine whether the lines L₁ : F(t) = (−2, 3, −1)t + (0,2,-3) and L2 : ƒ(s) = (2, −3, 1)s + (−10, 17, -8) intersect. If they do, find the point of intersection. ● They intersect at the point They are skew lines They are parallel or equalarrow_forwardAnswer number 15arrow_forward
- Why researchers are interested in describing measures of the center and measures of variation of a data set?arrow_forwardLet Χ be a real-valued character (mod k). Let k S = Σnx(n). n=1 If (a, k) = 1, ax(a)S = S (mod k). (iii) Write k = 2ºq where q is odd. Show that there is an integer a with (a, k) = 1 such that a = 3 (mod 2ª) and a = 2 (mod q). Deduce that 12S = 0 (mod k).arrow_forwardSolve for 14arrow_forward
- WHAT IS THE SOLUTION?arrow_forwardAnswer questions 2arrow_forwardThe following ordered data list shows the data speeds for cell phones used by a telephone company at an airport: A. Calculate the Measures of Central Tendency from the ungrouped data list. B. Group the data in an appropriate frequency table. C. Calculate the Measures of Central Tendency using the table in point B. 0.8 1.4 1.8 1.9 3.2 3.6 4.5 4.5 4.6 6.2 6.5 7.7 7.9 9.9 10.2 10.3 10.9 11.1 11.1 11.6 11.8 12.0 13.1 13.5 13.7 14.1 14.2 14.7 15.0 15.1 15.5 15.8 16.0 17.5 18.2 20.2 21.1 21.5 22.2 22.4 23.1 24.5 25.7 28.5 34.6 38.5 43.0 55.6 71.3 77.8arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,  College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning



