
(a)
Interpretation:
The probability of the presence of an electron at nucleus A in the bonding and also in the antibonding orbitals is to be calculated.
Concept introduction:
Electronic configuration tells about the arrangement of the electrons in each subshell and each orbital of an atom. The distribution of the electrons in the molecules is described by the molecular orbital theory. The unoccupied molecular orbital having lowest energy is known as the LUMO and the occupied molecular orbital having highest energy is known as the HOMO.
(a)
Answer to Problem 9B.2P
The probability of the presence of an electron at nucleus A in the bonding orbital is
Explanation of Solution
It is given that a small-electron probe having volume
The value of R is
The value of
The value of
The expression that is used represent probability of finding an electron is given below.
Where,
The distance between A and B is
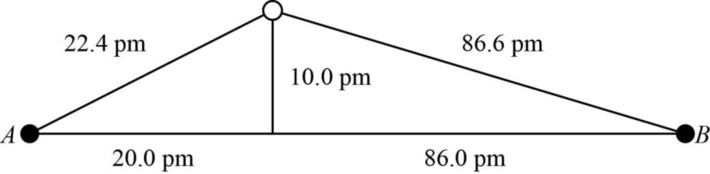
Figure 1
The value of
Substitute the values of
Substitute the values of
Therefore, the probability of the presence of an electron at nucleus A in the bonding orbital is
(b)
Interpretation:
The probability of the presence of an electron at nucleus B in the bonding and also in the antibonding orbitals is to be calculated.
Concept introduction:
Refer to part (a).
(b)
Answer to Problem 9B.2P
The probability of the presence of an electron at nucleus B in the bonding orbital is
Explanation of Solution
It is given that a small-electron probe having volume
The value of R is
The value of
The value of
The expression that is used represent probability of finding an electron is given below.
Where,
The distance between A and B is
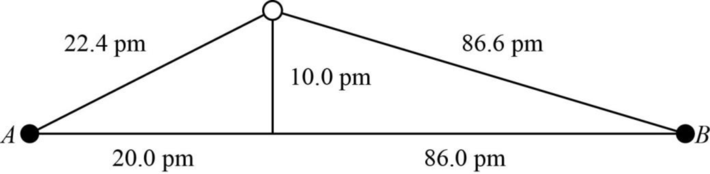
Figure 1
The value of
Substitute the values of
Substitute the values of
Therefore, the probability of the presence of an electron at nucleus B in the bonding orbital is
(c)
Interpretation:
The probability of the presence of an electron at half way between A and B in the bonding and also in the antibonding orbitals is to be calculated.
Concept introduction:
Refer to part (a).
(c)
Answer to Problem 9B.2P
The probability of the presence of an electron at half way between A and B in the bonding orbital is
Explanation of Solution
It is given that a small-electron probe having volume
The value of R is
The value of
The value of
The expression that is used represent probability of finding an electron is given below.
Where,
The distance between A and B is
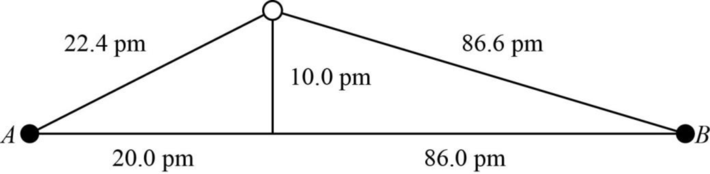
Figure 1
The value of
Substitute the values of
Substitute the values of
Therefore, the probability of the presence of an electron at half way between A and B in the bonding orbital is
(d)
Interpretation:
The probability of the presence of an electron at a point
Concept introduction:
Refer to part (a).
(d)
Answer to Problem 9B.2P
The probability of the presence of an electron at a point
Explanation of Solution
It is given that a small-electron probe having volume
The value of R is
The value of
The value of
The expression that is used represent probability of finding an electron is given below.
Where,
The distance between A and B is
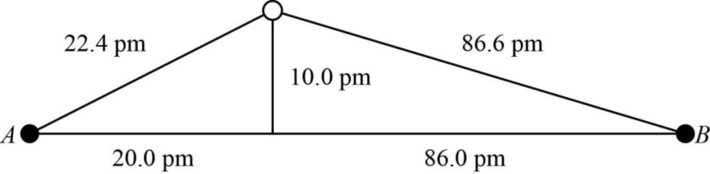
Figure 1
The value of
Substitute the values of
Substitute the values of
Therefore, the probability of the presence of an electron at a point
Want to see more full solutions like this?
Chapter 9 Solutions
Atkins' Physical Chemistry
- Identifying the major species in weak acid or weak base equilibria The preparations of two aqueous solutions are described in the table below. For each solution, write the chemical formulas of the major species present at equilibrium. You can leave out water itself. Write the chemical formulas of the species that will act as acids in the 'acids' row, the formulas of the species that will act as bases in the 'bases' row, and the formulas of the species that will act as neither acids nor bases in the 'other' row. You will find it useful to keep in mind that HF is a weak acid. 2.2 mol of NaOH is added to 1.0 L of a 1.4M HF solution. acids: П bases: Х other: ☐ ப acids: 0.51 mol of KOH is added to 1.0 L of a solution that is bases: 1.3M in both HF and NaF. other: ☐ 00. 18 Ararrow_forwardUsing reaction free energy to predict equilibrium composition Consider the following equilibrium: N2O4 (g) 2NO2 (g) AG⁰ = 5.4 kJ Now suppose a reaction vessel is filled with 1.68 atm of dinitrogen tetroxide (N204) at 148. °C. Answer the following questions about this system: rise Under these conditions, will the pressure of N2O4 tend to rise or fall? x10 fall Is it possible to reverse this tendency by adding NO2? In other words, if you said the pressure of N2O4 will tend to rise, can that be changed to a tendency to fall by adding NO2? Similarly, if you said the pressure of N2O4 will tend to fall, can that be changed to a tendency to rise by adding NO2? If you said the tendency can be reversed in the second question, calculate the minimum pressure of NO 2 needed to reverse it. Round your answer to 2 significant digits. yes no 0.42 atm ☑ 5 0/5 ? مله Ararrow_forwardHomework 13 (Ch17) Question 4 of 4 (1 point) | Question Attempt: 2 of 2 ✓ 1 ✓ 2 = 3 4 Time Remaining: 4:25:54 Using the thermodynamic information in the ALEKS Data tab, calculate the standard reaction free energy of the following chemical reaction: 2CH3OH (g)+302 (g) → 2CO2 (g) + 4H₂O (g) Round your answer to zero decimal places. ☐ kJ x10 ☐ Subm Check 2020 Hill LLC. All Rights Reserved. Terms of Use | Privacy Cearrow_forward
- Identifying the major species in weak acid or weak base equilibria Your answer is incorrect. • Row 2: Your answer is incorrect. • Row 3: Your answer is incorrect. • Row 6: Your answer is incorrect. 0/5 The preparations of two aqueous solutions are described in the table below. For each solution, write the chemical formulas of the major species present at equilibrium. You can leave out water itself. Write the chemical formulas of the species that will act as acids in the 'acids' row, the formulas of the species that will act as bases in the 'bases' row, and the formulas of the species that will act as neither acids nor bases in the 'other' row. You will find it useful to keep in mind that HF is a weak acid. acids: HF 0.1 mol of NaOH is added to 1.0 L of a 0.7M HF solution. bases: 0.13 mol of HCl is added to 1.0 L of a solution that is 1.0M in both HF and KF. Exponent other: F acids: HF bases: F other: K 1 0,0,... ? 000 18 Ararrow_forwardUsing reaction free energy to predict equilibrium composition Consider the following equilibrium: 2NOCI (g) 2NO (g) + Cl2 (g) AGº =41. kJ Now suppose a reaction vessel is filled with 4.50 atm of nitrosyl chloride (NOCI) and 6.38 atm of chlorine (C12) at 212. °C. Answer the following questions about this system: ? rise Under these conditions, will the pressure of NOCI tend to rise or fall? x10 fall Is it possible to reverse this tendency by adding NO? In other words, if you said the pressure of NOCI will tend to rise, can that be changed to a tendency to fall by adding NO? Similarly, if you said the pressure of NOCI will tend to fall, can that be changed to a tendency to rise by adding NO? yes no If you said the tendency can be reversed in the second question, calculate the minimum pressure of NO needed to reverse it. Round your answer to 2 significant digits. 0.035 atm ✓ G 00. 18 Ararrow_forwardHighlight each glycosidic bond in the molecule below. Then answer the questions in the table under the drawing area. HO- HO- -0 OH OH HO NG HO- HO- OH OH OH OH NG OHarrow_forward
- € + Suppose the molecule in the drawing area below were reacted with H₂ over a platinum catalyst. Edit the molecule to show what would happen to it. That is, turn it into the product of the reaction. Also, write the name of the product molecule under the drawing area. Name: ☐ H C=0 X H- OH HO- H HO- -H CH₂OH ×arrow_forwardDraw the Haworth projection of the disaccharide made by joining D-glucose and D-mannose with a ẞ(1-4) glycosidic bond. If the disaccharide has more than one anomer, you can draw any of them. Click and drag to start drawing a structure. Xarrow_forwardEpoxides can be opened in aqueous acid or aqueous base to produce diols (molecules with two OH groups). In this question, you'll explore the mechanism of epoxide opening in aqueous acid. 2nd attempt Be sure to show all four bonds at stereocenters using hash and wedge lines. 0 0 Draw curved arrows to show how the epoxide reacts with hydronium ion. 100 +1: 1st attempt Feedback Be sure to show all four bonds at stereocenters using hash and wedge lines. See Periodic Table See Hint H A 5 F F Hr See Periodic Table See Hintarrow_forward
- 03 Question (1 point) For the reaction below, draw both of the major organic products. Be sure to consider stereochemistry. > 1. CH₂CH₂MgBr 2. H₂O 3rd attempt Draw all four bonds at chiral centers. Draw all stereoisomers formed. Draw the structures here. e 130 AN H See Periodic Table See Hint P C Brarrow_forwardYou may wish to address the following issues in your response if they are pertinent to the reaction(s) you propose to employ:1) Chemoselectivity (why this functional group and not another?) 2) Regioselectivity (why here and not there?) 3) Stereoselectivity (why this stereoisomer?) 4) Changes in oxidation state. Please make it in detail and draw it out too in what step what happens. Thank you for helping me!arrow_forward1) Chemoselectivity (why this functional group and not another?) 2) Regioselectivity (why here and not there?) 3) Stereoselectivity (why this stereoisomer?) 4) Changes in oxidation state. Everything in detail and draw out and write it.arrow_forward
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education
ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning
Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education
Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY





