
Concept explainers
(a)
Describe puck’s coordinates x and y using Newton’s second law.
(a)
Answer to Problem 9.20P
Using Newton’s second law, the puck’s coordinates are
Explanation of Solution
Write the expression for the centrifugal force on puck,
Here,
Write the expression for the Coriolis force on puck,
Here,
Write the expression for the net force act on the puck,
Here,
Substitute (I) and (II) in (III),
Let us consider the turntable is along
Write the expression for the position vector,
Write the expression for the angular velocity,
(V) X (VI),
(VII) X (VI),
Write the expression for the linear velocity,
(IX) X (VI),
Substitute
Compare the above equation with (IX), and we get the equation for
Therefore, using Newton’s second law, the puck’s coordinates are
(b)
The general solution for the equation
(b)
Answer to Problem 9.20P
The general solution for the equation
Explanation of Solution
Write the given tricky expression,
Differentiate (XIV),
Again differentiate,
Substitute
Substitute
Consider the above equation in the form of
Rewrite the equation,
The general solution for this equation,
Here,
Therefore, the general solution for the equation
(c)
Show that the given equations.
(c)
Answer to Problem 9.20P
The given equations are proved here.
Explanation of Solution
From part (b),
Substitute
Since this constant does not depends on time.
So substitute
Differentiate the equation (XX) with respect to
Substitute
Substitute
Rewrite the above equation for
Substitute
Substitute
From the above equation, write the real part and imaginary part separately.
Therefore, the given equations are proved here.
(d)
Draw and describe the behavior of the puck when it has large
(d)
Answer to Problem 9.20P
The behavior of the puck when it has large
Explanation of Solution
Write the expression of motion for the coordinates x and y,
Here,
Let us write the functions,
Here,
Therefore, the equation (XXII) becomes,
In this case, the path of the puck should be spherical shape, because that circle is continuously growing at constant rate.
It is moving like a circle in a clockwise direction. The factor t explains that the circle grows at a constant rate. In this situation, the puck moves in a spiral orbit.
The figure 1 is the behavior of the puck.
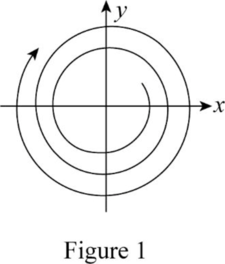
Therefore, the behavior of the puck when it has large
Want to see more full solutions like this?
- (1) Fm Fmn mn Fm B W₁ e Fmt W 0 Fit Wt 0 W Fit Fin n Fmt n As illustrated in Fig. consider the person performing extension/flexion movements of the lower leg about the knee joint (point O) to investigate the forces and torques produced by muscles crossing the knee joint. The setup of the experiment is described in Example above. The geometric parameters of the model under investigation, some of the forces acting on the lower leg and its free-body diagrams are shown in Figs. and For this system, the angular displacement, angular velocity, and angular accelera- tion of the lower leg were computed using data obtained during the experiment such that at an instant when 0 = 65°, @ = 4.5 rad/s, and a = 180 rad/s². Furthermore, for this sys- tem assume that a = 4.0 cm, b = 23 cm, ß = 25°, and the net torque generated about the knee joint is M₁ = 55 Nm. If the torque generated about the knee joint by the weight of the lower leg is Mw 11.5 Nm, determine: = The moment arm a of Fm relative to the…arrow_forwardThe figure shows a particle that carries a charge of 90 = -2.50 × 106 C. It is moving along the +y -> axis at a speed of v = 4.79 × 106 m/s. A magnetic field B of magnitude 3.24 × 10-5 T is directed along the +z axis, and an electric field E of magnitude 127 N/C points along the -x axis. Determine (a) the magnitude and (b) direction (as an angle within x-y plane with respect to +x- axis in the range (-180°, 180°]) of the net force that acts on the particle. +x +z AB 90 +yarrow_forwardThree charged particles are located at the corners of an equilateral triangle as shown in the figure below (let q = 1.00 μC, and L = 0.850 m). Calculate the total electric force on the 7.00-μC charge. magnitude direction N ° (counterclockwise from the +x axis) y 7.00 με 9 L 60.0° x -4.00 μC ①arrow_forward
- (a) Calculate the number of electrons in a small, electrically neutral silver pin that has a mass of 9.0 g. Silver has 47 electrons per atom, and its molar mass is 107.87 g/mol. (b) Imagine adding electrons to the pin until the negative charge has the very large value 1.00 mC. How many electrons are added for every 109 electrons already present?arrow_forward(a) A physics lab instructor is working on a new demonstration. She attaches two identical copper spheres with mass m = 0.180 g to cords of length L as shown in the figure. A Both spheres have the same charge of 6.80 nC, and are in static equilibrium when 0 = 4.95°. What is L (in m)? Assume the cords are massless. 0.180 Draw a free-body diagram, apply Newton's second law for a particle in equilibrium to one of the spheres. Find an equation for the distance between the two spheres in terms of L and 0, and use this expression in your Coulomb force equation. m (b) What If? The charge on both spheres is increased until each cord makes an angle of 0 = 9.90° with the vertical. If both spheres have the same electric charge, what is the charge (in nC) on each sphere in this case? 9.60 Use the same reasoning as in part (a), only now, use the length found in part (a) and the new angle to solve for the charge. ncarrow_forwardA proton moves at 5.20 x 105 m/s in the horizontal direction. It enters a uniform vertical electric field with a magnitude of 8.40 × 103 N/C. Ignore any gravitational effects. (a) Find the time interval required for the proton to travel 6.00 cm horizontally. 83.33 Your response differs from the correct answer by more than 10%. Double check your calculations. ns (b) Find its vertical displacement during the time interval in which it travels 6.00 cm horizontally. (Indicate direction with the sign of your answer.) 2.77 Your response differs from the correct answer by more than 10%. Double check your calculations. mm (c) Find the horizontal and vertical components of its velocity after it has traveled 6.00 cm horizontally. = 5.4e5 Your response differs significantly from the correct answer. Rework your solution from the beginning and check each step carefully. I + 6.68e4 Your response differs significantly from the correct answer. Rework your solution from the beginning and check each step…arrow_forward
- (a) A physics lab instructor is working on a new demonstration. She attaches two identical copper spheres with mass m = 0.180 g to cords of length L as shown in the figure. A Both spheres have the same charge of 6.80 nC, and are in static equilibrium when = 4.95°. What is L (in m)? Assume the cords are massless. 0.150 Draw a free-body diagram, apply Newton's second law for a particle in equilibrium to one of the spheres. Find an equation for the distance between the two spheres in terms of L and 0, and use this expression in your Coulomb force equation. m (b) What If? The charge on both spheres is increased until each cord makes an angle of 0 = 9.90° with the vertical. If both spheres have the same electric charge, what is the charge (in nC) on each sphere in this case? 13.6 ☑ Use the same reasoning as in part (a), only now, use the length found in part (a) and the new angle to solve for the charge. nCarrow_forwardA proton moves at 5.20 x 105 m/s in the horizontal direction. It enters a uniform vertical electric field with a magnitude of 8.40 × 10³ N/C. Ignore any gravitational effects. (a) Find the time interval required for the proton to travel 6.00 cm horizontally. 1.15e-7 ☑ Your response differs significantly from the correct answer. Rework your solution from the beginning and check each step carefully. ns (b) Find its vertical displacement during the time interval in which it travels 6.00 cm horizontally. (Indicate direction with the sign of your answer.) 5.33e-3 ☑ Your response is off by a multiple of ten. mm (c) Find the horizontal and vertical components of its velocity after it has traveled 6.00 cm horizontally. | ↑ + jkm/sarrow_forwardA proton moves at 5.20 105 m/s in the horizontal direction. It enters a uniform vertical electric field with a magnitude of 8.40 103 N/C. Ignore any gravitational effects. (a) Find the time interval required for the proton to travel 6.00 cm horizontally. (b) Find its vertical displacement during the time interval in which it travels 6.00 cm horizontally. (Indicate direction with the sign of your answer.)arrow_forward
- The figure below shows the electric field lines for two charged particles separated by a small distance. 92 91 (a) Determine the ratio 91/92. 1/3 × This is the correct magnitude for the ratio. (b) What are the signs of q₁ and 92? 91 positive 92 negative ×arrow_forwardPlease help me solve this one more detail, thanksarrow_forwardA dielectric-filled parallel-plate capacitor has plate area A = 20.0 ccm2 , plate separaton d = 10.0 mm and dielectric constant k = 4.00. The capacitor is connected to a battery that creates a constant voltage V = 12.5 V . Throughout the problem, use ϵ0 = 8.85×10−12 C2/N⋅m2 . Find the energy U1 of the dielectric-filled capacitor. The dielectric plate is now slowly pulled out of the capacitor, which remains connected to the battery. Find the energy U2 of the capacitor at the moment when the capacitor is half-filled with the dielectric. The capacitor is now disconnected from the battery, and the dielectric plate is slowly removed the rest of the way out of the capacitor. Find the new energy of the capacitor, U3. In the process of removing the remaining portion of the dielectric from the disconnected capacitor, how much work W is done by the external agent acting on the dielectric?arrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





