Chapter 9, Problem 78CE

The sodium content of a popular sports drink is listed as 220 mg in a 32-oz bottle. Analysis of 10 bottles indicates a sample mean of 228.2 mg with a sample standard deviation of 18.2 mg. (a) Write the hypotheses for a two-tailed test of the claimed sodium content. (b) Calculate the t test statistic to test the manufacturer’s claim. (c) At the 5 percent level of significance (α = .05), does the sample contradict the manufacturer’s claim? (d) Use Excel to find the p-value and compare it to the level of significance. Did you come to the same conclusion as you did in part (c)?

To determine

State the hypotheses for a two-tailed test of the claimed sodium content.

Answer to Problem 78CE

Null hypothesis:

$H_0:\mu =220\text{mg}$

Alternative hypothesis:

$H_1:\mu \ne 220\text{mg}$

Explanation of Solution

Calculation:

The given information is that, the mean and standard deviation for a sample of 10 bottles is 228.2 mg and 18.2 mg. That is, $\overline{x}=228.2$, $n=10$ and $s=18.2$.

Here, the claim is that the sodium content in a 32-oz bottle is 220 mg.

State the hypotheses for a two-tailed test:

Null hypothesis:

$H_0:\mu =220\text{mg}$

That is, the sodium content in a 32-oz bottle is 220 mg.

Alternative hypothesis:

$H_1:\mu \ne 220\text{mg}$

That is, the sodium content in a 32-oz bottle is not 220 mg.

To determine

Find the t test statistic to test the claim.

Answer to Problem 78CE

The test statistic is 1.4248.

Explanation of Solution

Calculation:

Test statistic:

The formula for test statistic is,

$t_{\text{calc}}=\frac{\overline{x}-{\mu }_0}{\frac{s}{\sqrt{n}}}$

Where $\overline{x}$ is the sample mean, ${\mu }_0$ is the population mean, s is the sample standard deviation and n is the sample size.

Substitute $\overline{x}=228.2$, ${\mu }_0=220$, $s=18.2$ and $n=10$ in the test statistic formula.

$\begin{array}{c}{t}_{\text{calc}}=\frac{228.2-220}{\frac{18.2}{\sqrt{10}}}\\ =\frac{8.2}{\left(\frac{18.2}{3.16228}\right)}\\ =\frac{8.2}{5.7553}\\ =1.4248\end{array}$

Thus, the test statistic is 1.4248.

To determine

Check whether the sample contradict the manufacturer’s claim or not.

Answer to Problem 78CE

The sample do not contradict the manufacturer’s claim.

Explanation of Solution

Calculation:

Critical value:

For two tailed test,

$\begin{array}{c}1-\frac{\alpha }{2}=1-\frac{0.05}{2}\\ =0.975\end{array}$

Degrees of freedom:

$\begin{array}{c}df=n-1\\ =10-1\\ =9\end{array}$

Critical value:

Software procedure:

Step-by-step software procedure to obtain critical value using EXCEL is as follows:

• Open an EXCEL file.
• In cell A1, enter the formula “=T.INV(0.975, 9)”
• Output using EXCEL software is given below:

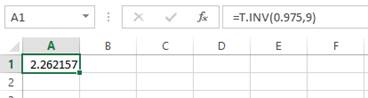
Thus, the critical value of Student’s t is $t_{0.025}=\pm 2.262$.

Decision rule for two-tailed test at $\alpha =0.05$:

If $t_{\text{calc}}>+2.262$, then reject the null hypothesis.

If $t_{\text{calc}}<-2.262$, then reject the null hypothesis.

Conclusion for critical value method:

Here, the test statistic is greater than the critical value.

That is, $t_{\text{calc}}\left(=1.4248\right)<2.262$.

Therefore, the null hypothesis is not rejected.

Hence, the sample does not contradict the manufacturer’s claim. That is, there is evidence to infer that the sodium content in a 32-oz bottle is 220 mg.

To determine

Find the p-value by using Excel and compare it to the level of significance. Also, check the conclusion for p-value method provide the same conclusion as did in part (c).

Answer to Problem 78CE

The p-value is 0.1880.

The conclusion is that, the sample does not contradict the manufacturer’s claim.

Yes, the conclusion for critical value method and p-value method are same.

Explanation of Solution

Calculation:

p-value:

Software procedure:

Step-by-step software procedure to obtain p-value using EXCEL is as follows:

• Open an EXCEL file.
• In cell A1, enter the formula “=T.DIST.2T(1.4248,9)”.
• Output using Excel software is given below:

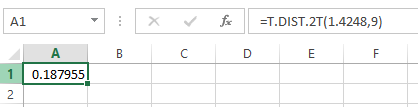
Thus, the p-value is 0.1880.

Decision rule:

If $p\text{-value}<\alpha$, then reject the null hypothesis.

Conclusion for p-value method:

Here, the p-value is greater than the level of significance.

That is, $p\text{-value}\left(=0.1880\right)>\alpha \left(=0.05\right)$.

Therefore, the null hypothesis is not rejected.

Hence, the sample do not contradict the manufacturer’s claim. That is, there is evidence to infer that the sodium content in a 32-oz bottle is 220 mg. Moreover, the conclusion for critical value method and p-value method are same.