
(a)
To explain: The
(a)
Explanation of Solution
A line segment with a particular direction running from initial point to terminal point is called a vector in the plane. A vector in the plane is denoted by
The vector
Where,
A vector represents a magnitude and a direction.
(b)
To find: The vector with initial point
(b)
Answer to Problem 1RCC
The vector with initial point
Explanation of Solution
Given:
The initial point is
Formula used:
The formula to calculate the vector
Calculation:
Substitute 2 for
Thus, the vector with initial point
(c)
The terminal point of the vector
(c)
Answer to Problem 1RCC
The terminal point of the vector
Explanation of Solution
Given:
The vector
Calculation:
Section (a):
The terminal point of
Substitute x for
Compare both sides,
Thus, the terminal point of the vector
Section (b):
Draw the graph of vector as shown below,
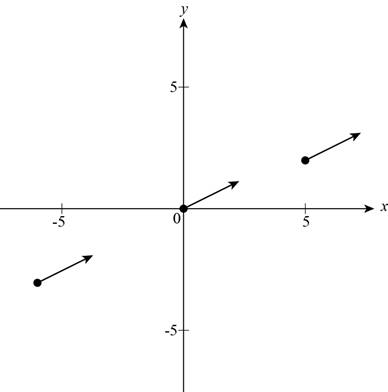
Figure (1)
Thus, Figure (1) shows various representations of the vector
(d)
The definition of magnitude of vector and the value of the vector
(d)
Explanation of Solution
Calculation:
The length of the line segment is called the magnitude of the vector and it is denoted by
The magnitude of the vector
Thus, magnitude of vector
(e)
The vectors
(e)
Explanation of Solution
Calculation:
A vector of length 1 is called a unit vector. The vectors
The vector
Thus, the vector
(f)
The direction
(f)
Explanation of Solution
Calculation:
The smallest positive angle in standard position formed by the positive x-axis and the vector
The vector
And
Where,
The vector
The graph for the above equation is,
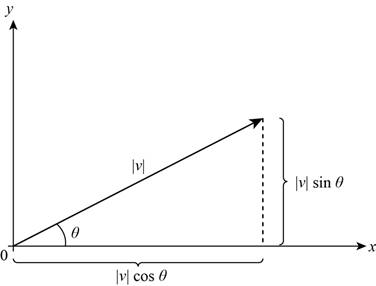
Figure (2)
Thus, Figure (2) shows the graph of the coordinates of a vector in terms of length and direction.
(g)
To find: The vector
(g)
Answer to Problem 1RCC
The vector
Explanation of Solution
Given:
The length
Calculation:
The vector
And
Substitute 5 for
And
Substitute
Thus, the coordinates of the vector
Want to see more full solutions like this?
Chapter 9 Solutions
PRECALCULUS
- 2. Find a matrix A with the following qualities a. A is 3 x 3. b. The matrix A is not lower triangular and is not upper triangular. c. At least one value in each row is not a 1, 2,-1, -2, or 0 d. A is invertible.arrow_forwardFind the exact area inside r=2sin(2\theta ) and outside r=\sqrt(3)arrow_forwardA 20 foot ladder rests on level ground; its head (top) is against a vertical wall. The bottom of the ladder begins by being 12 feet from the wall but begins moving away at the rate of 0.1 feet per second. At what rate is the top of the ladder slipping down the wall? You may use a calculator.arrow_forward
- Explain the key points and reasons for the establishment of 12.3.2(integral Test)arrow_forwardUse 12.4.2 to determine whether the infinite series on the right side of equation 12.6.5, 12.6.6 and 12.6.7 converges for every real number x.arrow_forwarduse Cauchy Mean-Value Theorem to derive Corollary 12.6.2, and then derive 12.6.3arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning  Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,




