
(a)
To explain: The
(a)
Explanation of Solution
A line segment with a particular direction running from initial point to terminal point is called a vector in the plane. A vector in the plane is denoted by
The vector
Where,
A vector represents a magnitude and a direction.
(b)
To find: The vector with initial point
(b)
Answer to Problem 1RCC
The vector with initial point
Explanation of Solution
Given:
The initial point is
Formula used:
The formula to calculate the vector
Calculation:
Substitute 2 for
Thus, the vector with initial point
(c)
The terminal point of the vector
(c)
Answer to Problem 1RCC
The terminal point of the vector
Explanation of Solution
Given:
The vector
Calculation:
Section (a):
The terminal point of
Substitute x for
Compare both sides,
Thus, the terminal point of the vector
Section (b):
Draw the graph of vector as shown below,
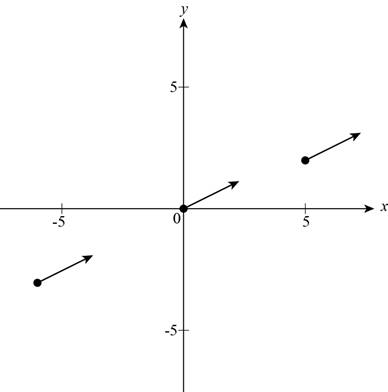
Figure (1)
Thus, Figure (1) shows various representations of the vector
(d)
The definition of magnitude of vector and the value of the vector
(d)
Explanation of Solution
Calculation:
The length of the line segment is called the magnitude of the vector and it is denoted by
The magnitude of the vector
Thus, magnitude of vector
(e)
The vectors
(e)
Explanation of Solution
Calculation:
A vector of length 1 is called a unit vector. The vectors
The vector
Thus, the vector
(f)
The direction
(f)
Explanation of Solution
Calculation:
The smallest positive angle in standard position formed by the positive x-axis and the vector
The vector
And
Where,
The vector
The graph for the above equation is,
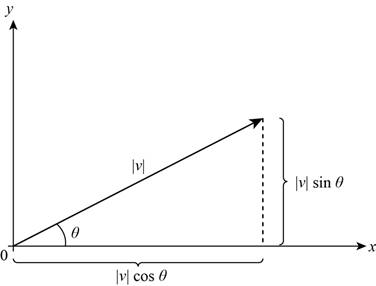
Figure (2)
Thus, Figure (2) shows the graph of the coordinates of a vector in terms of length and direction.
(g)
To find: The vector
(g)
Answer to Problem 1RCC
The vector
Explanation of Solution
Given:
The length
Calculation:
The vector
And
Substitute 5 for
And
Substitute
Thus, the coordinates of the vector
Want to see more full solutions like this?
Chapter 9 Solutions
PRECALCULUS VOL. 1 W/ENH. WEBASSIGN >I
- Find the total area of the shaded regions. y 18- 16- 14- 12- 10- 8- 6- y=ex+1-e 4- 2- 0- 2 3 4 5 -2 -4- X ☑ The total area of the shaded regions is (Type an integer or decimal rounded to three decimal places as needed.)arrow_forwardThe graph of f(x), shown here, consists of two straight line segments and two quarter circles. Find the 19 value of f(x)dx. 小 Srxdx. 19 f(x)dx y 7 -7 2 12 19 X ☑arrow_forwardCan you solve this two numerical method eqn and teach me.arrow_forward
- Find the area between the following curves. x=-4, x=2, y=ex, and y = 3 - ex Set up the integral (or integrals) needed to compute this area. Use the small (Type exact answers in terms of e.) 3 In 2 A. S √ [3-2e*] dx+ -4 2 S [2ex-3] dx 3 In 2 B. dx Find the area between the curves. Area = (Type an exact answer in terms of e.)arrow_forwardUse the definite integral to find the area between the x-axis and f(x) over the indicated interval. Check first to see if the graph crosses the x-axis in the given interval. f(x)=8-2x²: [0,4] Set up the integral (or integrals) needed to compute this area. Use the smallest possible number of integrals. Select the correct choice below and fill in the answer boxes to ○ A. dx B. 2 S 8-2x² dx+ 4 S 2 8-2x2 dx C. dx + S dx For the interval [0,4], the area between the x-axis and f(x) is (Type an integer or a simplified fraction.)arrow_forwardPollution from a factory is entering a lake. The rate of concentration of the pollutant at time t is 5 given by P'(t) = 126t², where t is the number of years since the factory started introducing pollutants into the lake. Ecologists estimate that the lake can accept a total level of pollution of 600 units before all the fish life in the lake ends. Can the factory operate for 2 years without killing all the fish in the lake? Set up the integral that would determine the pollution level after 2 years. 2 5 126t 2 dt Can the factory operate for 2 years without killing all the fish in the lake? Thee factory can operate for 2 years without killing all the fish in the lake because the value of the integral is , which is less than 600. (Round to the nearest integer as needed.)arrow_forward
- Use the definite integral to find the area between the x-axis and f(x) over the indicated interval. Check first to see if the graph crosses the x-axis in the given interval. f(x)=4x-12; [2,6] The area between the x-axis and f(x) is (Type an integer or a simplified fraction.)arrow_forwardEvaluate the definite integral. 70 √5√2-6 3 dz 70 S 5√2-6 dz= 7 江 (Type an integer or decimal rounded to two decimal places as needed.)arrow_forwardFind the area between the following curves. 2 y=x³-x²+x+4; y=5x² -7x+4 The area between the curves is (Simplify your answer.) ...arrow_forward
- Find the area of the shaded region. 3- -1 -3- Q The total area of the shaded regions is (Simplify your answer.) y=9-x² Q 1 3 5 Xarrow_forwardFind the area of the region bounded by the graphs of the given equations. y=17x, y=x² ... The area is (Type an integer or a simplified fraction.)arrow_forwardFind the area between the curves. y=x-26, y=9-2x ... The area between the curves is (Type an integer or decimal rounded to the nearest tenth as needed.)arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning  Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,




