
(a)
To explain: The
(a)
Explanation of Solution
A line segment with a particular direction running from initial point to terminal point is called a vector in the plane. A vector in the plane is denoted by
The vector
Where,
A vector represents a magnitude and a direction.
(b)
To find: The vector with initial point
(b)
Answer to Problem 1RCC
The vector with initial point
Explanation of Solution
Given:
The initial point is
Formula used:
The formula to calculate the vector
Calculation:
Substitute 2 for
Thus, the vector with initial point
(c)
The terminal point of the vector
(c)
Answer to Problem 1RCC
The terminal point of the vector
Explanation of Solution
Given:
The vector
Calculation:
Section (a):
The terminal point of
Substitute x for
Compare both sides,
Thus, the terminal point of the vector
Section (b):
Draw the graph of vector as shown below,
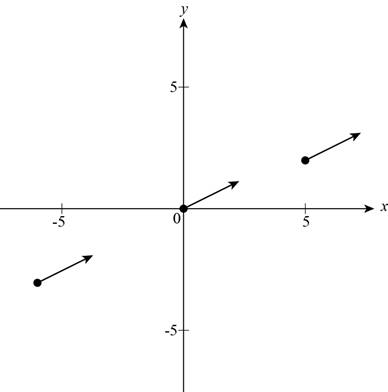
Figure (1)
Thus, Figure (1) shows various representations of the vector
(d)
The definition of magnitude of vector and the value of the vector
(d)
Explanation of Solution
Calculation:
The length of the line segment is called the magnitude of the vector and it is denoted by
The magnitude of the vector
Thus, magnitude of vector
(e)
The vectors
(e)
Explanation of Solution
Calculation:
A vector of length 1 is called a unit vector. The vectors
The vector
Thus, the vector
(f)
The direction
(f)
Explanation of Solution
Calculation:
The smallest positive angle in standard position formed by the positive x-axis and the vector
The vector
And
Where,
The vector
The graph for the above equation is,
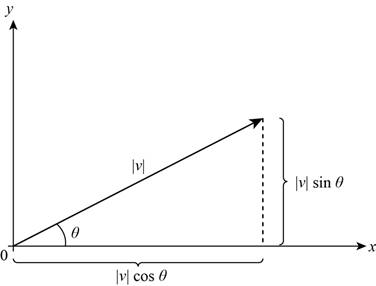
Figure (2)
Thus, Figure (2) shows the graph of the coordinates of a vector in terms of length and direction.
(g)
To find: The vector
(g)
Answer to Problem 1RCC
The vector
Explanation of Solution
Given:
The length
Calculation:
The vector
And
Substitute 5 for
And
Substitute
Thus, the coordinates of the vector
Want to see more full solutions like this?
Chapter 9 Solutions
Student Solutions Manual for Stewart/Redlin/Watson's Precalculus: Mathematics for Calculus, 7th
- 1. 3 2 fx=14x²-15x²-9x- 2arrow_forwardNo it is not a graded assignment, its a review question but i only have the final answer not the working or explanationarrow_forwardClass, the class silues, and the class notes, whether the series does alternate and the absolute values of the terms decrease), and if the test does apply, determine whether the series converges or diverges. For the ith series, if the test does not apply the let Mi = 2, while if the test determines divergence then M¿ = 4, and if it determines convergence then M¿ = 8. 1: 2: 3 : 4: 5 : ∞ n=1 ∞ (−1)n+1. Σ(-1) +1 n=1 ∞ п 3m² +2 Σ(-1)+1 sin(2n). n=1 ∞ 2n² + 2n +3 4n2 +6 1 e-n + n² 3n23n+1 9n² +3 In(n + 1) 2n+1 Σ(-1) +1 n=1 ∞ Σ(-1)". n=1 Then the value of cos(M₁) + cos(2M2) + cos(3M3) + sin(2M4) + sin(M5) is 1.715 0.902 0.930 -1.647 -0.057 ● 2.013 1.141 4.274arrow_forward
- 3. FCX14) = x²+3xx-y3 +.arrow_forwardA cylindrical chemical storage tank with a capacity of 950m3 is going to be constructed in a warehouse that is 11m by 14m with a height of 10m. The specifications call for the case to be made of sheet metal that costs $90/m2, the top to be made from sheet metal that costs $45/m2 and the wall to be made of sheet metal that costs $80/m2. If you want to minimize the cost to make the storage house, how much would you end up spending to build the tank?arrow_forwardCalculate the max value of the directional derivatearrow_forward
- Calculus III May I please have the example, definition semicolons, and all blanks completed and solved? Thank you so much,arrow_forwardA company estimates that the revenue (in dollars) from the sale of x doghouses is given by R(x) = 12,000 In (0.02x+1). Use the differential to approximate the change in revenue from the sale of one more doghouse if 80 doghouses have already been sold. The revenue will increase by $ if one more doghouse is made. (Round to the nearest cent as needed.)arrow_forwardThe population of bacteria (in millions) in a certain culture x hours after an experimental 20x nutrient is introduced into the culture is P(x) = - 2 Use the differential to approximate the changes in population for the following changes in x. 8+x a. 1 to 1.5 b. 3 to 3.25 a. Use the differential to approximate the change in population for x=1 to 1.5. Between 1 and 1.5 hours, the population of bacteria changes by million. (Round to three decimal places as needed.)arrow_forward
- The demand for grass seed (in thousands of pounds) at price p dollars is given by the following function. D(p) 3p³-2p² + 1460 Use the differential to approximate the changes in demand for the following changes in p. a. $4 to $4.11 b. $6 to $6.19arrow_forwardLet the region R be the area enclosed by the function f(x) = 3 ln (x) and g(x) = 3 x + 1. Write an integral in terms of x and also an integral in terms of y that would represent the area of the region R. If necessary, round limit values to the nearest thousandth. Answer Attempt 1 out of 2 y 7 10 6 5 4 3 2 -1 2 3 4 5 6 x2 dx x1 = x2 = x1 Y1 = Y2 = Y1 dyarrow_forwardA manufacturer of handcrafted wine racks has determined that the cost to produce x units per month is given by C = 0.3x² + 7,000. How fast is the cost per month changing when production is changing at the rate of 14 units per month and the production level is 80 units? Costs are increasing at the rate of $ (Round to the nearest dollar as needed.) per month at this production level.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning  Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,




