Calculus
7th Edition
ISBN: 9781524916817
Author: SMITH KARL J, STRAUSS MONTY J, TODA MAGDALENA DANIELE
Publisher: Kendall Hunt Publishing
expand_more
expand_more
format_list_bulleted
Question
Chapter 9, Problem 1PE
(a)
To determine
To find:a
(a)
Expert Solution
Explanation of Solution
A Vector is a quantity that has both magnitude and direction. A vector PQ is represented as a directed line segment and an arrow with initial point
A vector is indicated by writing an arrow over the designated points
Vector PQ is the vector from
Conclusion:
Therefore, a Vector is a quantity that has both magnitude and direction.
(b)
To determine
To find: a scalar.
(b)
Expert Solution
Explanation of Solution
A scalar is a quantity that has only magnitude, not direction. In context of vectors, a scalar is described as a real number.
For example,
Conclusion:
Therefore, a scalar is a quantity that has only magnitude, not direction.
(c)
To determine
To give: an algebraic and a geometric interpretation of multiplication of a vector by a scalar.
(c)
Expert Solution
Explanation of Solution
When a scalar number c is multiplied by a vector v , the scalar multiple cv will be parallel to the vector v and has length
The scalar multiple cv points in the same direction as v if
Geometrically, assume that vector v has a magnitude of 3 units and its direction is from point P to point Q .
The scalar multiple 2v will have a magnitude of
Conclusion:
Therefore,when a scalar number c is multiplied by a vector v , the scalar multiple cv will be parallel to the vector v and has length
Geometrically, the scalar multiple 2v will have a magnitude of
(d)
To determine
To find: parallelogram rule for vector sums
(d)
Expert Solution
Explanation of Solution
The Parallelogram rule states that
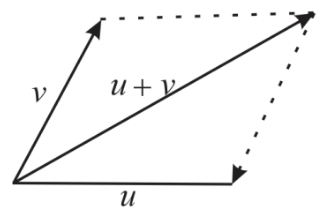
Conclusion:
Therefore, the Parallelogram rule states that
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Find the tangent line approximation 7 to the graph of f at the given point.
T(x) =
f(x) = csc(x), (8, csc(8))
Complete the table. (Round your answers to four decimal places.)
x
f(x)
T(x)
7.9
7.99
8
8.01
8.1
Can you solve it numerical method
Use the information to find and compare Ay and dy. (Round your answers to four decimal places.)
Function
x-Value
Differential of x
Ду
=
dy
=
y = x² + 2
x = -4
Ax = dx = 0.01
Chapter 9 Solutions
Calculus
Ch. 9.1 - Prob. 1PSCh. 9.1 - Prob. 2PSCh. 9.1 - Prob. 3PSCh. 9.1 - Prob. 4PSCh. 9.1 - Prob. 5PSCh. 9.1 - Prob. 6PSCh. 9.1 - Prob. 7PSCh. 9.1 - Prob. 8PSCh. 9.1 - Prob. 9PSCh. 9.1 - Prob. 10PS
Ch. 9.1 - Prob. 11PSCh. 9.1 - Prob. 12PSCh. 9.1 - Prob. 13PSCh. 9.1 - Prob. 14PSCh. 9.1 - Prob. 15PSCh. 9.1 - Prob. 16PSCh. 9.1 - Prob. 17PSCh. 9.1 - Prob. 18PSCh. 9.1 - Prob. 19PSCh. 9.1 - Prob. 20PSCh. 9.1 - Prob. 21PSCh. 9.1 - Prob. 22PSCh. 9.1 - Prob. 23PSCh. 9.1 - Prob. 24PSCh. 9.1 - Prob. 25PSCh. 9.1 - Prob. 26PSCh. 9.1 - Prob. 27PSCh. 9.1 - Prob. 28PSCh. 9.1 - Prob. 29PSCh. 9.1 - Prob. 30PSCh. 9.1 - Prob. 31PSCh. 9.1 - Prob. 32PSCh. 9.1 - Prob. 33PSCh. 9.1 - Prob. 34PSCh. 9.1 - Prob. 35PSCh. 9.1 - Prob. 36PSCh. 9.1 - Prob. 37PSCh. 9.1 - Prob. 38PSCh. 9.1 - Prob. 39PSCh. 9.1 - Prob. 40PSCh. 9.1 - Prob. 41PSCh. 9.1 - Prob. 42PSCh. 9.1 - Prob. 43PSCh. 9.1 - Prob. 44PSCh. 9.1 - Prob. 45PSCh. 9.1 - Prob. 46PSCh. 9.1 - Prob. 47PSCh. 9.1 - Prob. 48PSCh. 9.1 - Prob. 49PSCh. 9.1 - Prob. 50PSCh. 9.1 - Prob. 51PSCh. 9.1 - Prob. 52PSCh. 9.1 - Prob. 53PSCh. 9.1 - Prob. 54PSCh. 9.1 - Prob. 55PSCh. 9.1 - Prob. 56PSCh. 9.1 - Prob. 57PSCh. 9.1 - Prob. 58PSCh. 9.1 - Prob. 59PSCh. 9.1 - Prob. 60PSCh. 9.2 - Prob. 1PSCh. 9.2 - Prob. 2PSCh. 9.2 - Prob. 3PSCh. 9.2 - Prob. 4PSCh. 9.2 - Prob. 5PSCh. 9.2 - Prob. 6PSCh. 9.2 - Prob. 7PSCh. 9.2 - Prob. 8PSCh. 9.2 - Prob. 9PSCh. 9.2 - Prob. 10PSCh. 9.2 - Prob. 11PSCh. 9.2 - Prob. 12PSCh. 9.2 - Prob. 13PSCh. 9.2 - Prob. 14PSCh. 9.2 - Prob. 15PSCh. 9.2 - Prob. 16PSCh. 9.2 - Prob. 17PSCh. 9.2 - Prob. 18PSCh. 9.2 - Prob. 19PSCh. 9.2 - Prob. 20PSCh. 9.2 - Prob. 21PSCh. 9.2 - Prob. 22PSCh. 9.2 - Prob. 23PSCh. 9.2 - Prob. 24PSCh. 9.2 - Prob. 25PSCh. 9.2 - Prob. 26PSCh. 9.2 - Prob. 27PSCh. 9.2 - Prob. 28PSCh. 9.2 - Prob. 29PSCh. 9.2 - Prob. 30PSCh. 9.2 - Prob. 31PSCh. 9.2 - Prob. 32PSCh. 9.2 - Prob. 33PSCh. 9.2 - Prob. 34PSCh. 9.2 - Prob. 35PSCh. 9.2 - Prob. 36PSCh. 9.2 - Prob. 37PSCh. 9.2 - Prob. 38PSCh. 9.2 - Prob. 39PSCh. 9.2 - Prob. 40PSCh. 9.2 - Prob. 41PSCh. 9.2 - Prob. 42PSCh. 9.2 - Prob. 43PSCh. 9.2 - Prob. 44PSCh. 9.2 - Prob. 45PSCh. 9.2 - Prob. 46PSCh. 9.2 - Prob. 47PSCh. 9.2 - Prob. 48PSCh. 9.2 - Prob. 49PSCh. 9.2 - Prob. 50PSCh. 9.2 - Prob. 51PSCh. 9.2 - Prob. 52PSCh. 9.2 - Prob. 53PSCh. 9.2 - Prob. 54PSCh. 9.2 - Prob. 55PSCh. 9.2 - Prob. 56PSCh. 9.2 - Prob. 57PSCh. 9.2 - Prob. 58PSCh. 9.2 - Prob. 59PSCh. 9.2 - Prob. 60PSCh. 9.3 - Prob. 1PSCh. 9.3 - Prob. 2PSCh. 9.3 - Prob. 3PSCh. 9.3 - Prob. 4PSCh. 9.3 - Prob. 5PSCh. 9.3 - Prob. 6PSCh. 9.3 - Prob. 7PSCh. 9.3 - Prob. 8PSCh. 9.3 - Prob. 9PSCh. 9.3 - Prob. 10PSCh. 9.3 - Prob. 11PSCh. 9.3 - Prob. 12PSCh. 9.3 - Prob. 13PSCh. 9.3 - Prob. 14PSCh. 9.3 - Prob. 15PSCh. 9.3 - Prob. 16PSCh. 9.3 - Prob. 17PSCh. 9.3 - Prob. 18PSCh. 9.3 - Prob. 19PSCh. 9.3 - Prob. 20PSCh. 9.3 - Prob. 21PSCh. 9.3 - Prob. 22PSCh. 9.3 - Prob. 23PSCh. 9.3 - Prob. 24PSCh. 9.3 - Prob. 25PSCh. 9.3 - Prob. 26PSCh. 9.3 - Prob. 27PSCh. 9.3 - Prob. 28PSCh. 9.3 - Prob. 29PSCh. 9.3 - Prob. 30PSCh. 9.3 - Prob. 31PSCh. 9.3 - Prob. 32PSCh. 9.3 - Prob. 33PSCh. 9.3 - Prob. 34PSCh. 9.3 - Prob. 35PSCh. 9.3 - Prob. 36PSCh. 9.3 - Prob. 37PSCh. 9.3 - Prob. 38PSCh. 9.3 - Prob. 39PSCh. 9.3 - Prob. 40PSCh. 9.3 - Prob. 41PSCh. 9.3 - Prob. 42PSCh. 9.3 - Prob. 43PSCh. 9.3 - Prob. 44PSCh. 9.3 - Prob. 45PSCh. 9.3 - Prob. 46PSCh. 9.3 - Prob. 47PSCh. 9.3 - Prob. 48PSCh. 9.3 - Prob. 49PSCh. 9.3 - Prob. 50PSCh. 9.3 - Prob. 51PSCh. 9.3 - Prob. 52PSCh. 9.3 - Prob. 53PSCh. 9.3 - Prob. 54PSCh. 9.3 - Prob. 55PSCh. 9.3 - Prob. 56PSCh. 9.3 - Prob. 57PSCh. 9.3 - Prob. 58PSCh. 9.3 - Prob. 59PSCh. 9.3 - Prob. 60PSCh. 9.4 - Prob. 1PSCh. 9.4 - Prob. 2PSCh. 9.4 - Prob. 3PSCh. 9.4 - Prob. 4PSCh. 9.4 - Prob. 5PSCh. 9.4 - Prob. 6PSCh. 9.4 - Prob. 7PSCh. 9.4 - Prob. 8PSCh. 9.4 - Prob. 9PSCh. 9.4 - Prob. 10PSCh. 9.4 - Prob. 11PSCh. 9.4 - Prob. 12PSCh. 9.4 - Prob. 13PSCh. 9.4 - Prob. 14PSCh. 9.4 - Prob. 15PSCh. 9.4 - Prob. 16PSCh. 9.4 - Prob. 17PSCh. 9.4 - Prob. 18PSCh. 9.4 - Prob. 19PSCh. 9.4 - Prob. 20PSCh. 9.4 - Prob. 21PSCh. 9.4 - Prob. 22PSCh. 9.4 - Prob. 23PSCh. 9.4 - Prob. 24PSCh. 9.4 - Prob. 25PSCh. 9.4 - Prob. 26PSCh. 9.4 - Prob. 27PSCh. 9.4 - Prob. 28PSCh. 9.4 - Prob. 29PSCh. 9.4 - Prob. 30PSCh. 9.4 - Prob. 31PSCh. 9.4 - Prob. 32PSCh. 9.4 - Prob. 33PSCh. 9.4 - Prob. 34PSCh. 9.4 - Prob. 35PSCh. 9.4 - Prob. 36PSCh. 9.4 - Prob. 37PSCh. 9.4 - Prob. 38PSCh. 9.4 - Prob. 39PSCh. 9.4 - Prob. 40PSCh. 9.4 - Prob. 41PSCh. 9.4 - Prob. 42PSCh. 9.4 - Prob. 43PSCh. 9.4 - Prob. 44PSCh. 9.4 - Prob. 45PSCh. 9.4 - Prob. 46PSCh. 9.4 - Prob. 47PSCh. 9.4 - Prob. 48PSCh. 9.4 - Prob. 49PSCh. 9.4 - Prob. 50PSCh. 9.4 - Prob. 51PSCh. 9.4 - Prob. 52PSCh. 9.4 - Prob. 53PSCh. 9.4 - Prob. 54PSCh. 9.4 - Prob. 55PSCh. 9.4 - Prob. 56PSCh. 9.4 - Prob. 57PSCh. 9.4 - Prob. 58PSCh. 9.4 - Prob. 59PSCh. 9.4 - Prob. 60PSCh. 9.5 - Prob. 1PSCh. 9.5 - Prob. 2PSCh. 9.5 - Prob. 3PSCh. 9.5 - Prob. 4PSCh. 9.5 - Prob. 5PSCh. 9.5 - Prob. 6PSCh. 9.5 - Prob. 7PSCh. 9.5 - Prob. 8PSCh. 9.5 - Prob. 9PSCh. 9.5 - Prob. 10PSCh. 9.5 - Prob. 11PSCh. 9.5 - Prob. 12PSCh. 9.5 - Prob. 13PSCh. 9.5 - Prob. 14PSCh. 9.5 - Prob. 15PSCh. 9.5 - Prob. 16PSCh. 9.5 - Prob. 17PSCh. 9.5 - Prob. 18PSCh. 9.5 - Prob. 19PSCh. 9.5 - Prob. 20PSCh. 9.5 - Prob. 21PSCh. 9.5 - Prob. 22PSCh. 9.5 - Prob. 23PSCh. 9.5 - Prob. 24PSCh. 9.5 - Prob. 25PSCh. 9.5 - Prob. 26PSCh. 9.5 - Prob. 27PSCh. 9.5 - Prob. 28PSCh. 9.5 - Prob. 29PSCh. 9.5 - Prob. 30PSCh. 9.5 - Prob. 31PSCh. 9.5 - Prob. 32PSCh. 9.5 - Prob. 33PSCh. 9.5 - Prob. 34PSCh. 9.5 - Prob. 35PSCh. 9.5 - Prob. 36PSCh. 9.5 - Prob. 37PSCh. 9.5 - Prob. 38PSCh. 9.5 - Prob. 39PSCh. 9.5 - Prob. 40PSCh. 9.5 - Prob. 41PSCh. 9.5 - Prob. 42PSCh. 9.5 - Prob. 43PSCh. 9.5 - Prob. 44PSCh. 9.5 - Prob. 45PSCh. 9.5 - Prob. 46PSCh. 9.5 - Prob. 47PSCh. 9.5 - Prob. 48PSCh. 9.5 - Prob. 49PSCh. 9.5 - Prob. 50PSCh. 9.5 - Prob. 51PSCh. 9.5 - Prob. 52PSCh. 9.5 - Prob. 53PSCh. 9.5 - Prob. 54PSCh. 9.5 - Prob. 55PSCh. 9.5 - Prob. 56PSCh. 9.5 - Prob. 57PSCh. 9.5 - Prob. 58PSCh. 9.5 - Prob. 59PSCh. 9.5 - Prob. 60PSCh. 9.6 - Prob. 1PSCh. 9.6 - Prob. 2PSCh. 9.6 - Prob. 3PSCh. 9.6 - Prob. 4PSCh. 9.6 - Prob. 5PSCh. 9.6 - Prob. 6PSCh. 9.6 - Prob. 7PSCh. 9.6 - Prob. 8PSCh. 9.6 - Prob. 9PSCh. 9.6 - Prob. 10PSCh. 9.6 - Prob. 11PSCh. 9.6 - Prob. 12PSCh. 9.6 - Prob. 13PSCh. 9.6 - Prob. 14PSCh. 9.6 - Prob. 15PSCh. 9.6 - Prob. 16PSCh. 9.6 - Prob. 17PSCh. 9.6 - Prob. 18PSCh. 9.6 - Prob. 19PSCh. 9.6 - Prob. 20PSCh. 9.6 - Prob. 21PSCh. 9.6 - Prob. 22PSCh. 9.6 - Prob. 23PSCh. 9.6 - Prob. 24PSCh. 9.6 - Prob. 25PSCh. 9.6 - Prob. 26PSCh. 9.6 - Prob. 27PSCh. 9.6 - Prob. 28PSCh. 9.6 - Prob. 29PSCh. 9.6 - Prob. 30PSCh. 9.6 - Prob. 31PSCh. 9.6 - Prob. 32PSCh. 9.6 - Prob. 33PSCh. 9.6 - Prob. 34PSCh. 9.6 - Prob. 35PSCh. 9.6 - Prob. 36PSCh. 9.6 - Prob. 37PSCh. 9.6 - Prob. 38PSCh. 9.6 - Prob. 39PSCh. 9.6 - Prob. 40PSCh. 9.6 - Prob. 41PSCh. 9.6 - Prob. 42PSCh. 9.6 - Prob. 43PSCh. 9.6 - Prob. 44PSCh. 9.6 - Prob. 45PSCh. 9.6 - Prob. 46PSCh. 9.6 - Prob. 47PSCh. 9.6 - Prob. 48PSCh. 9.6 - Prob. 49PSCh. 9.6 - Prob. 50PSCh. 9.6 - Prob. 51PSCh. 9.6 - Prob. 52PSCh. 9.6 - Prob. 53PSCh. 9.6 - Prob. 54PSCh. 9.6 - Prob. 55PSCh. 9.6 - Prob. 56PSCh. 9.6 - Prob. 57PSCh. 9.6 - Prob. 58PSCh. 9.6 - Prob. 59PSCh. 9.6 - Prob. 60PSCh. 9.7 - Prob. 1PSCh. 9.7 - Prob. 2PSCh. 9.7 - Prob. 3PSCh. 9.7 - Prob. 4PSCh. 9.7 - Prob. 5PSCh. 9.7 - Prob. 6PSCh. 9.7 - Prob. 7PSCh. 9.7 - Prob. 8PSCh. 9.7 - Prob. 9PSCh. 9.7 - Prob. 10PSCh. 9.7 - Prob. 11PSCh. 9.7 - Prob. 12PSCh. 9.7 - Prob. 13PSCh. 9.7 - Prob. 14PSCh. 9.7 - Prob. 15PSCh. 9.7 - Prob. 16PSCh. 9.7 - Prob. 17PSCh. 9.7 - Prob. 18PSCh. 9.7 - Prob. 19PSCh. 9.7 - Prob. 20PSCh. 9.7 - Prob. 21PSCh. 9.7 - Prob. 22PSCh. 9.7 - Prob. 23PSCh. 9.7 - Prob. 24PSCh. 9.7 - Prob. 25PSCh. 9.7 - Prob. 26PSCh. 9.7 - Prob. 27PSCh. 9.7 - Prob. 28PSCh. 9.7 - Prob. 29PSCh. 9.7 - Prob. 30PSCh. 9.7 - Prob. 31PSCh. 9.7 - Prob. 32PSCh. 9.7 - Prob. 33PSCh. 9.7 - Prob. 34PSCh. 9.7 - Prob. 35PSCh. 9.7 - Prob. 36PSCh. 9.7 - Prob. 37PSCh. 9.7 - Prob. 38PSCh. 9.7 - Prob. 39PSCh. 9.7 - Prob. 40PSCh. 9.7 - Prob. 41PSCh. 9.7 - Prob. 42PSCh. 9.7 - Prob. 43PSCh. 9.7 - Prob. 44PSCh. 9.7 - Prob. 45PSCh. 9.7 - Prob. 46PSCh. 9.7 - Prob. 47PSCh. 9.7 - Prob. 48PSCh. 9.7 - Prob. 49PSCh. 9.7 - Prob. 50PSCh. 9.7 - Prob. 51PSCh. 9.7 - Prob. 52PSCh. 9.7 - Prob. 53PSCh. 9.7 - Prob. 54PSCh. 9.7 - Prob. 55PSCh. 9.7 - Prob. 56PSCh. 9.7 - Prob. 57PSCh. 9.7 - Prob. 58PSCh. 9.7 - Prob. 59PSCh. 9.7 - Prob. 60PSCh. 9 - Prob. 1PECh. 9 - Prob. 2PECh. 9 - Prob. 3PECh. 9 - Prob. 4PECh. 9 - Prob. 5PECh. 9 - Prob. 6PECh. 9 - Prob. 7PECh. 9 - Prob. 8PECh. 9 - Prob. 9PECh. 9 - Prob. 10PECh. 9 - Prob. 11PECh. 9 - Prob. 12PECh. 9 - Prob. 13PECh. 9 - Prob. 14PECh. 9 - Prob. 15PECh. 9 - Prob. 16PECh. 9 - Prob. 17PECh. 9 - Prob. 18PECh. 9 - Prob. 19PECh. 9 - Prob. 20PECh. 9 - Prob. 21PECh. 9 - Prob. 22PECh. 9 - Prob. 23PECh. 9 - Prob. 24PECh. 9 - Prob. 25PECh. 9 - Prob. 26PECh. 9 - Prob. 27PECh. 9 - Prob. 28PECh. 9 - Prob. 29PECh. 9 - Prob. 30PECh. 9 - Prob. 1SPCh. 9 - Prob. 2SPCh. 9 - Prob. 3SPCh. 9 - Prob. 4SPCh. 9 - Prob. 5SPCh. 9 - Prob. 6SPCh. 9 - Prob. 7SPCh. 9 - Prob. 8SPCh. 9 - Prob. 9SPCh. 9 - Prob. 10SPCh. 9 - Prob. 11SPCh. 9 - Prob. 12SPCh. 9 - Prob. 13SPCh. 9 - Prob. 14SPCh. 9 - Prob. 15SPCh. 9 - Prob. 16SPCh. 9 - Prob. 17SPCh. 9 - Prob. 18SPCh. 9 - Prob. 19SPCh. 9 - Prob. 20SPCh. 9 - Prob. 21SPCh. 9 - Prob. 22SPCh. 9 - Prob. 23SPCh. 9 - Prob. 24SPCh. 9 - Prob. 25SPCh. 9 - Prob. 26SPCh. 9 - Prob. 27SPCh. 9 - Prob. 28SPCh. 9 - Prob. 29SPCh. 9 - Prob. 30SPCh. 9 - Prob. 31SPCh. 9 - Prob. 32SPCh. 9 - Prob. 33SPCh. 9 - Prob. 34SPCh. 9 - Prob. 35SPCh. 9 - Prob. 36SPCh. 9 - Prob. 37SPCh. 9 - Prob. 38SPCh. 9 - Prob. 39SPCh. 9 - Prob. 40SPCh. 9 - Prob. 41SPCh. 9 - Prob. 42SPCh. 9 - Prob. 43SPCh. 9 - Prob. 44SPCh. 9 - Prob. 45SPCh. 9 - Prob. 46SPCh. 9 - Prob. 47SPCh. 9 - Prob. 48SPCh. 9 - Prob. 49SPCh. 9 - Prob. 50SPCh. 9 - Prob. 51SPCh. 9 - Prob. 52SPCh. 9 - Prob. 53SPCh. 9 - Prob. 54SPCh. 9 - Prob. 55SPCh. 9 - Prob. 56SPCh. 9 - Prob. 57SPCh. 9 - Prob. 58SPCh. 9 - Prob. 59SPCh. 9 - Prob. 60SPCh. 9 - Prob. 61SPCh. 9 - Prob. 62SPCh. 9 - Prob. 63SPCh. 9 - Prob. 64SPCh. 9 - Prob. 65SPCh. 9 - Prob. 66SPCh. 9 - Prob. 67SPCh. 9 - Prob. 68SPCh. 9 - Prob. 69SPCh. 9 - Prob. 70SPCh. 9 - Prob. 71SPCh. 9 - Prob. 72SPCh. 9 - Prob. 73SPCh. 9 - Prob. 74SPCh. 9 - Prob. 75SPCh. 9 - Prob. 76SPCh. 9 - Prob. 77SPCh. 9 - Prob. 78SPCh. 9 - Prob. 79SPCh. 9 - Prob. 80SPCh. 9 - Prob. 81SPCh. 9 - Prob. 82SPCh. 9 - Prob. 83SPCh. 9 - Prob. 84SPCh. 9 - Prob. 85SPCh. 9 - Prob. 86SPCh. 9 - Prob. 87SPCh. 9 - Prob. 88SPCh. 9 - Prob. 89SPCh. 9 - Prob. 90SPCh. 9 - Prob. 91SPCh. 9 - Prob. 92SPCh. 9 - Prob. 93SPCh. 9 - Prob. 94SPCh. 9 - Prob. 95SPCh. 9 - Prob. 96SPCh. 9 - Prob. 97SPCh. 9 - Prob. 98SPCh. 9 - Prob. 99SP
Knowledge Booster
Similar questions
- Calculus lll May I please have the statements with blank lines completed; furthermore, may I please have the text box completed? Thank youarrow_forwardCalculus lll May I please have the statements completed for the following text lines and box? Thank you so much,arrow_forwardCalculus lll May I please have the solution for the following exercise? Thank you so mucharrow_forward
- Calculus lll May I please have the statement completed for the following box? Thank you so much,arrow_forwardCalculus lll May I please have the solution for the following exercise? Thank you so mucharrow_forwardUse a graphing calculator to find where the curves intersect and to find the area between the curves. y=ex, y=-x²-4x a. The left point of intersection is (Type integers or decimals rounded to the nearest thousandth as needed. Type an ordered pair.)arrow_forward
- Find the area between the curves. x= -5, x=3, y=2x² +9, y=0 The area between the curves is (Round to the nearest whole number as needed.)arrow_forwardcan you solve these questions with step by step with clear explaination pleasearrow_forwardFind the area between the following curves. x=-1, x=3, y=x-1, and y=0 The area between the curves is (Simplify your answer.)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning